Basic Rules of Triangle
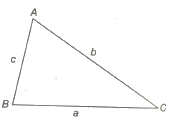
In ΔABC, the angles are denoted by capital letters A, Band C and the lengths of the sides opposite to these angles are denoted by small letters a, b and c, respectively. Semi-perimeter of the triangle is written as
s= a + b + c / 2
and area denoted by Δ.
(i) Sine Rule sin A / a = sin B / b = sin C / c = 1 / 2R, where R is the radius of the circumstances of the ΔABC.
(ii) Cosine Rule
cos A = b2 + c2 – a2 / 2bc
cos B = a2 + c2 – b2 / 2ac
cos C = a2 + b2 – c2 / 2ab
(iii) Projection Rule a = b cos C + c cos B,
b = c cos A + a cos C and c = a cos B + b cos A
(iV) Napier’s Analogy tan B – C / 2 = b – c / b + c cot A / 2,
tan C – A / 2 = c – a / c + a cot B / 2 and tan A – B / 2 = a – b / a + b cot C / 2
Trigonometrical Ratios of Half of the Angles
Area of Triangles
Consider a triangle of side a, b and c.
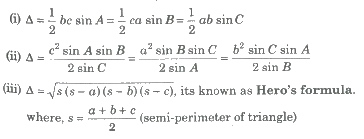
(iv) Δ = abc / 4R = rs
where, R and r are the radii of the circumcircle and the incircle of the ΔABC, respectively.
Solution of Triangles
Elements of a Triangle
There are six elements of a triangle, in which three are its sides and other three are its angle.
If three elements of a triangle are given, atleast one of which is its side; then other elements can be uniquely calculated. This is called solving the triangle.
1. Solutions of a Right Angled Triangle
Let ΔABC be a given triangle with right angle at C, then
(i) solution when two sides are given
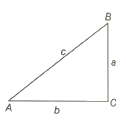
(ii) solution when one side and one a cute angle are given
2. Solutions of a Triangle in General
(i) Solution when three sides a, band c are given, then
sin A = 2Δ / bc, sin B = 2Δ / ac, sin C = 2Δ / ab
where, Δ = √s(s – a)(s – b)(s – c) and s = a + b + c / 2
and A + B + C = 180°
(ii) Solution when two sides and the included angle are given, then
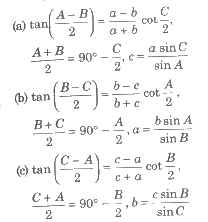
This is called as Napier’s analogy.
(iii) Solution when one side a and two angles A and B are given, then
C = 180° – (A + B)
b = c sin B / sin C and C = sin C / sin A
(iv) Solution when two sides a, b and the opposite ∠A is given, then
sin B = b / a sin A, C = 180° – (A + B), c = a sin C / sin A
Now, different cases arises here.
(a) If A is an acute angle and a < b sin A, then sin B = b / a sin A gives sin B > 1, which is not possible, so no such triangle is possible.
(b) When A is an acute angle and a = b sin A In this case, only one triangle is possible, which is right angled at B.
(c) If A is an acute angle and a > b sin A In this case, there are two values of B given by
sin B = b sin A / a, say B1 and B2 such that B1 + B2 = 180°,
side c can be calculated from
c = a sin C / sin A
Circles Connected with Triangle
1. Circumcircle
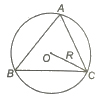
The circle passing through the vertices of the ΔABC is called the circumcircle. Its radius R is called the circumradius.
R = a / 2 sin A = b / 2 sin B = c / 2 sin C = abc / 4 Δ
2.Incircle
The circle touches the three sides of the A triangle internally is called the inscribed or the incircle of the triangle. Its radius r is called inradius of the circle.
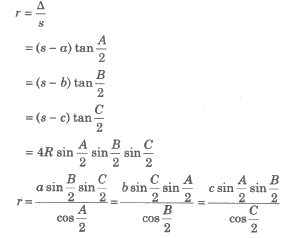
3. Escribed Circle
The circle touches BC and the two sides AB and AC produced of ΔABC externally is called the escribed circle opposite A. Its radius is denoted by rl.
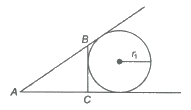
similarly, r2 and r3 denote the radii of the escribed circles opposite angles Band C, respectively. Hence, rl, r2 and r3 are called the exradius of &DeltaABC. Here,
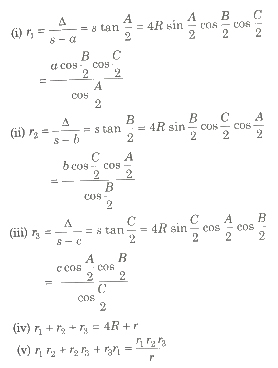
4. Orthocentre and Pedal Triangle
The point of intersection of perpendicular drawn from the vertices on the opposite sides of a triangle is called orthocentre.
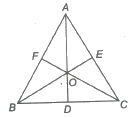
The ΔDEF formed by joining the feet of the altitudes is called the pedal triangle.
(i) Distance of the orthocentre of the triangle from the angular points are 2R cos A, 2R co~ B, 2R cos C and its distances from the sides are 2 R cos B cos C, 2 R cos C cos A, 2 R cos A cos B.
(ii) The length of medians AD, BE and CF of a Δ ABC are
AD = 1 / 2 √2b2 + 2c2 – a2
BE 1 / 2 √2c2 + 2a2 – b2
CF = 1 / 2 √2a2 + 2b2 – c2
Radii of the Inscribed and Circumscribed Circles of Regular Polygon
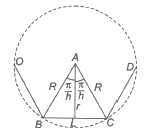
(i) R = a / 2 cosec π / n
(ii) r = a / 2 cot π / n, where a is the length of a side of polygon.
(iii) The area of the polygon = n (Area of AABC)
= 1 / 4na2 cot (π / n)
= nr2 tan π / n = n / 2 R2 sin (2π / n)
Some Properties of Triangle
(i) The mid-point of the hypotenuse of a right angled triangle is equidistant from the three vertices of the triangle.
(ii) The mid-point of the hypotenuse of a right angled triangle is the circumcentre of the triangle.
(iii) If any triangle, the exterior angle is equal to the sum of interior opposite angles.
(iv) In a Δ ABC, if DE||AB, then
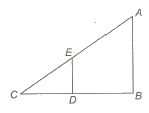
AB / DE = BC / DC = AC / EC
(v) In any Δ ABC, if AD is the angle bisector of ∠ BAC, then
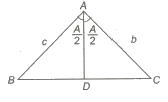
BD / DC = AB / AC = c / b
(vi) Appollonius Theorem If AD is median of the &dELTA; ABC, then
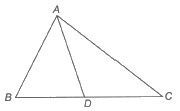
AB2 + AC2 = 2 (AD2 + BD2)
(vii) m-n Theorem In a ΔABC, D is a A point on the line BC such that BD : DC= m: n and ∠ADC = θ, ∠BAD = α, ∠DAC = β, then
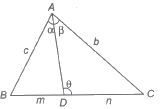
(a) (m + n) cot θ = m cot α – n cot β
(b) (m + n) cot θ = n cot B – m cot C
(viii) In an isosceles triangle, the median is perpendicular to the base.
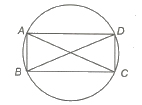
(ix) ptolemy’s Theorem In a cyclic quadrilateral ABCD
AB x CD + AD x BC = AC x BD
Heights and Distances
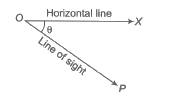
Angle of Elevation
If O be the observer’s eye and OX be the p horizontal line through O. If the object P is at higher level than eye, then ∠POX is called the angle of elevation.
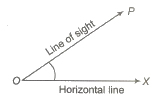
Angle of Depression
If the object P is a lower level than O, then ∠POX is called the angle of depression.
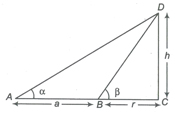
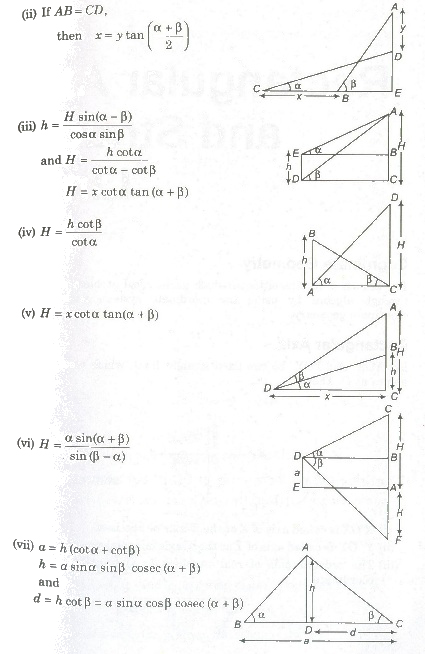
Important Results on Height and Distance
(i) a = h (cot α – cot β)
| « Click Here for Previous Topic | Click Here for Next Topic » |
Click Here for CBSE Class 11 Maths All Chapters Notes
To get fastest exam alerts and government job alerts in India, join our Telegram channel.
Discussion about this post