Class 12 Maths Indefinite Integrals – Get here the Notes for Class 12 Maths Indefinite Integrals. Candidates who are ambitious to qualify the Class 12 with good score can check this article for Notes. This is possible only when you have the best CBSE Class 12 Maths study material and a smart preparation plan. To assist you with that, we are here with notes. Hope these notes will helps you understand the important topics and remember the key points for exam point of view. Below we provided the Notes of Class 12 Maths for topic Indefinite Integrals.
- Class: 12th
- Subject: Maths
- Topic: Indefinite Integrals
- Resource: Notes
CBSE Notes Class 12 Maths Indefinite Integrals
Candidates who are pursuing in Class 12 are advised to revise the notes from this post. With the help of Notes, candidates can plan their Strategy for particular weaker section of the subject and study hard. So, go ahead and check the Important Notes for Class 12 Maths Indefinite Integrals
Let f(x) be a function. Then, the collection of all its primitives is called the indefinite integral of f(x) and is denoted by ∫f(x)dx. Integration as inverse operation of differentiation. If d/dx {φ(x)) = f(x), ∫f(x)dx = φ(x) + C, where C is called the constant of integration or arbitrary constant.
Symbols f(x) → Integrand
f(x)dx → Element of integration
∫→ Sign of integral
φ(x) → Anti-derivative or primitive or integral of function f(x)
The process of finding functions whose derivative is given, is called anti-differentiation or integration.

Elementary Standard Integrals
Geometrical Interpretation of Indefinite Integral
If d/dx {φ(x)} = f (x), then ∫f(x)dx = φ(x) + C. For different values of C, we get different functions, differing only by a constant. The graphs of these functions give us an infinite family of curves such that at the points on these curves with the same x-coordinate, the tangents are parallel as they have the same slope φ'(x) = f(x).
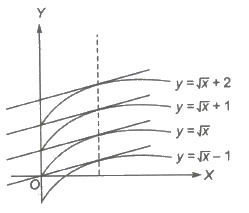
Consider the integral of 1/2√x
i.e., ∫1/2√xdx = √x + C, C ∈ R
Above figure shows some members of the family of curves given by y = + C for different C ∈ R.
Comparison between Differentiation and Integration
(i) Both differentiation and integration are linear operator on functions as
d/dx {af(x) ± bg(x)} = a d/dx{f(x) ± d/dx{g(x)}
and ∫[a.f(x) ± b.g(x)dx = a ∫f(x)dx ± b ∫g(x)dx
(ii) All functions are not differentiable, similarly there are some function which are not integrable.
(iii) Integral of a function is always discussed in an interval but derivative of a function can be discussed in a interval as well as on a point.
(iv) Geometrically derivative of a function represents slope of the tangent to the graph of function at the point. On the other hand, integral of a function represents an infinite family of curves placed parallel to each other having parallel tangents at points of intersection of the curves with a line parallel to Y-axis.
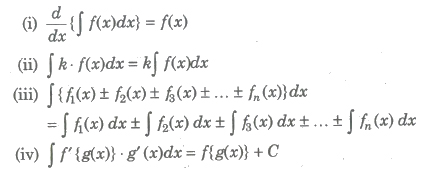
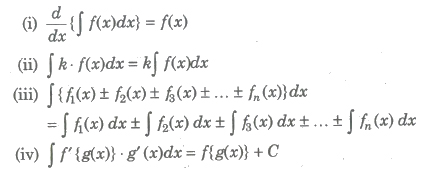
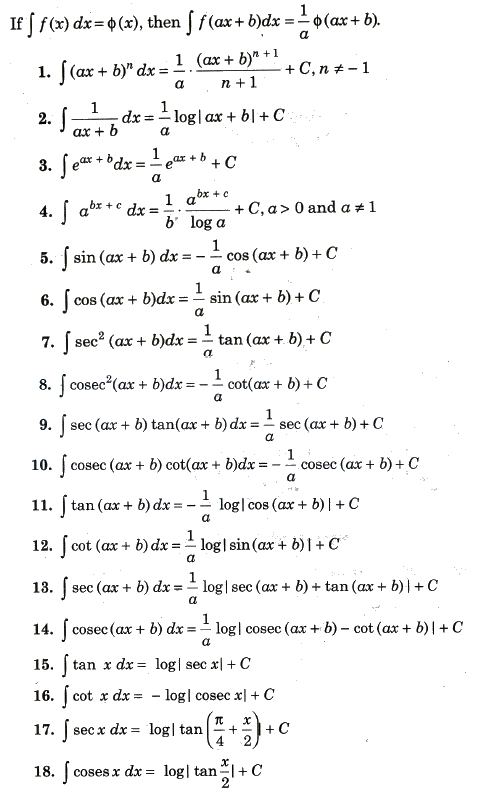
Rules of Integration
Method of Substitution
Basic Formulae Using Method of Substitution
If degree of the numerator of the integrand is equal to or greater than that of denominator divide the numerator by the denominator until the degree of the remainder is less than that of denominator i.e.,
(Numerator / Denominator) = Quotient + (Remainder / Denominator)
Trigonometric Identities Used for Conversion of Integrals into the Integrable Forms
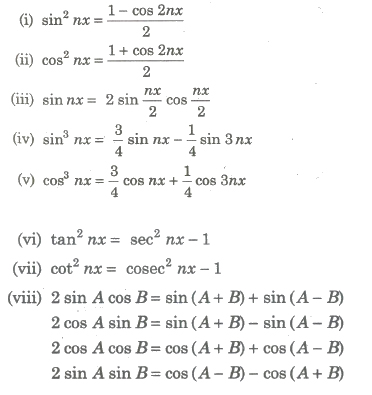
Standard Substitution

Special Integrals
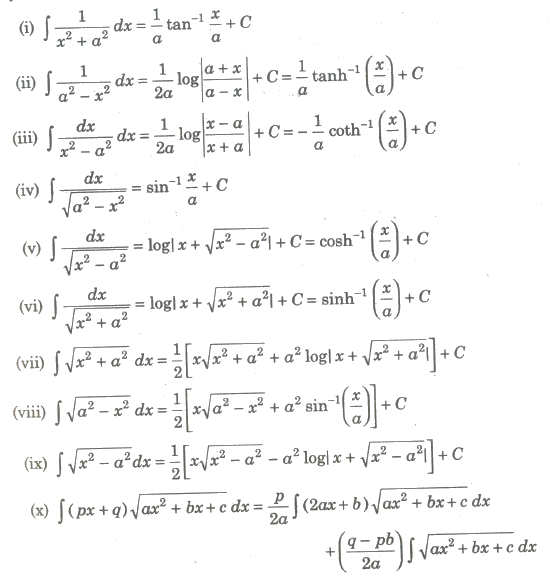
Important Forms to be converted into Special Integrals
(i) Form I
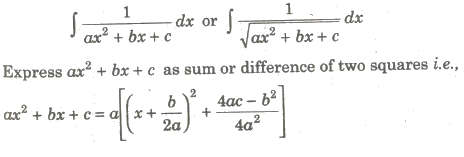
(ii) Form II
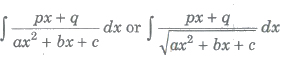
Put px + q = λd / dx (ax2 + bx + c) + mu;
Now, find values of λ and mu; and integrate.
(iii) Form III
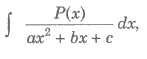
when P(x) is a polynomial of degree 2 or more carry out the dimension and express in the form
P(x) / (ax2 + bx + c) = Q(x) + R(x) / (ax2 + bx + c), where R(x) is a linear expression or constant, then integral reduces to the form discussed earlier.
(iv) Form IV
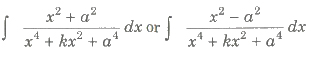
After dividing both numerator and denominator by x2, put x – a2 / x = t or x + (a2 / x) = t.
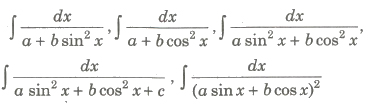
(v) Form V
To evaluate the above type of integrals, we proceed as follow
(a) Divide numerator and denominator by cos2x.
(b) Rreplace sec2x, if any in denominator by 1 + tan2 x.
(c) Put tan x = t, then sec2xdx = dt
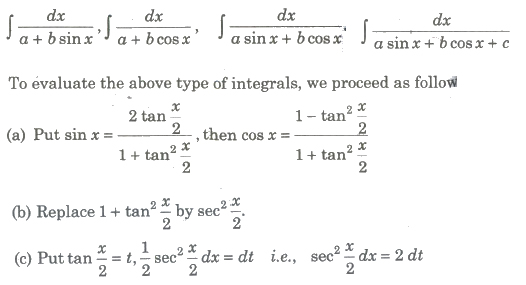
(vi) Form VI

(vii) Form VII
(viii) Form VIII

(ix) Form IX
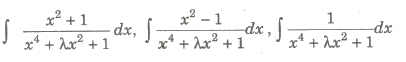
To evaluate the above type of integrals, we proceed as follows
- Divide numerator and denominator by x2
- Express the denominator of integrands in the form of (x + 1/x)2 ± k2
- Introduce (x + 1/x) or d (x – 1/x) or both in numerator.
- Put x + 1/x = t or x – 1/x = t as the case may be.
- Integral reduced to the form of ∫ 1 / x2 + a2dx or ∫ 1 / x2 + a2dx
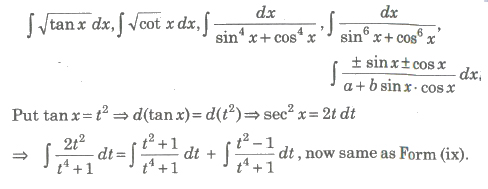
(x) Form X
Integration by Parts
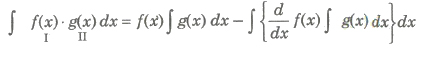
This method is used to integrate the product of two functions. If f(x) and g(x) be two integrable functions, then
(i) We use the following preferential order for taking the first function. Inverse→ Logarithm→ Algebraic → Trigonometric→ Exponential. In short we write it HATE.
(ii) If one of the function is not directly integrable, then we take it a the first function.
(iii) If only one function is there, i.e., ∫log x dx, then 1 (unity) is taken as second function.
(iv) If both the functions are directly integrable, then the first function is chosen in such a way that its derivative vanishes easily or the function obtained in integral sign is easilY integrable.
Integral of the Form
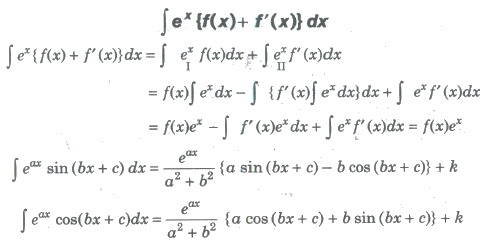
Integration Using Partial Fractions
(i) If f(x) and g(x) are two polynomials, then f(x) / g(x) defines a rational algebraic function of x. If degree of f(x) < degree of g(x), then f(x) / g(x) is called a proper rational function.
(ii) If degree of f(x) ≥ degree of g(x), then f(x) /g(x) is called an improper g(x) rational function.
(iii) If f(x) / g(x) isan improper rational function, then we divide f(x) by g(x) g(x) and convert it into a proper rational function as f(x) / g(x) = φ(x) + h(x) / g(x).
(iv) Any proper rational function f(x) / g(x) can be expressed as the sum of rational functions each having a simple factor of g(x). Each such fraction is called a partial fraction and the process of obtaining them, is called the resolution or decomposition of f(x) /g(x) partial fraction.

Shortcut for Finding Values of A, B and C etc.
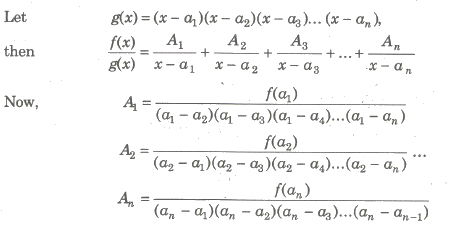
Case I. When g(x) is expressible as the product of non-repeated line factors.
Trick To find Ap put x = a in numerator and denominator after P deleting the factor (x — ap).
Case II. When g(x) is expressible as product of repeated linear factors.
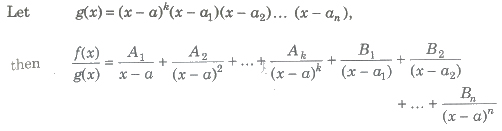
Here, all the constant cannot be calculated by using the method in Case I. However, Bl, B2, B3, … , Bn can be found using the same method i.e., shortcut can be applied only in the case of non-repeated linear factor.
Integration of Irrational Algebraic Function
Irrational function of the form of (ax + b)1/n and x can be evaluated by substitution (ax + b) = tn, thus

Integrals of the Type (bxm + bxn)P
Case I. If P ∈ N (natural number) we expand the binomial theorem and integrate.
Case II. If P ∈ Z (integers), put x = pk, where k denominator of m and n.
Case III. If (m+1)/n is an integer, we put (a + bxn) = rk, where k is th denominator of the fraction.
Integration of Hyperbolic Functions
- ∫sinh x dx = cosh x + C
- ∫cosh x dx = sinh x + C
- ∫sech2x dx = tanh x + C
- ∫cosech2x dx = – coth x + C
- ∫sech x tanh x dx = – sech x + C
- ∫cosech x coth x dx = – cosech x + C
Case IV If {(m+1)/n} + P is an integer, we put (a + bxn) = rkxn is the denominator of the fraction p.

Class 12 Key Points, Important Questions & Practice Papers
Hope these notes helped you in your schools exam preparation. Candidates can also check out the Key Points, Important Questions & Practice Papers for various Subjects for Class 12 in both Hindi and English language form the link below.
Class 12 NCERT Solutions
Candidates who are studying in Class 12 can also check Class 12 NCERT Solutions from here. This will help the candidates to know the solutions for all subjects covered in Class 12th. Candidates can click on the subject wise link to get the same. Class 12 Chapter-wise, detailed solutions to the questions of the NCERT textbooks are provided with the objective of helping students compare their answers with the sample answers.
Class 12 Mock Test / Practice
Mock test are the practice test or you can say the blue print of the main exam. Before appearing in the main examination, candidates must try mock test as it helps the students learn from their mistakes. With the help of Class 12 Mock Test / Practice, candidates can also get an idea about the pattern and marking scheme of that examination. For the sake of the candidates we are providing Class 12 Mock Test / Practice links below.
Class 12 Exemplar Questions
Exemplar Questions Class 12 is a very important resource for students preparing for the Examination. Here we have provided Exemplar Problems Solutions along with NCERT Exemplar Problems Class 12. Question from very important topics is covered by Exemplar Questions for Class 12.
Class 12 Maths
Chemistry Notes Physics Notes Biology Notes
To get study material, exam alerts and news, join our Whatsapp Channel.


