Class 12 Maths Definite Integrals and its Application – Get here the Notes for Class 12 Maths Definite Integrals and its Application. Candidates who are ambitious to qualify the Class 12 with good score can check this article for Notes. This is possible only when you have the best CBSE Class 12 Maths study material and a smart preparation plan. To assist you with that, we are here with notes. Hope these notes will helps you understand the important topics and remember the key points for exam point of view. Below we provided the Notes of Class 12 Maths for topic Definite Integrals and its Application.
- Class: 12th
- Subject: Maths
- Topic: Definite Integrals and its Application
- Resource: Notes
CBSE Notes Class 12 Maths Definite Integrals and its Application
Candidates who are pursuing in Class 12 are advised to revise the notes from this post. With the help of Notes, candidates can plan their Strategy for particular weaker section of the subject and study hard. So, go ahead and check the Important Notes for Class 12 Maths Definite Integrals and its Application
Let f(x) be a function defined on the interval [a, b] and F(x) be its anti-derivative. Then,
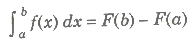
The above is called the second fundamental theorem of calculus.
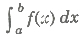
is defined as the definite integral of f(x) from x = a to x = b. The numbers and b are called limits of integration. We write
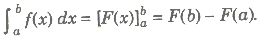
Evaluation of Definite Integrals by Substitution
Consider a definite integral of the following form
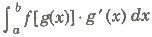
Step 1 Substitute g(x) = t
⇒ g ‘(x) dx = dt
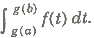
Step 2 Find the limits of integration in new system of variable i.e.. the lower limit is g(a) and the upper limit is g(b) and the g(b) integral is now
Step 3 Evaluate the integral, so obtained by usual method.
properties of Definite Integral
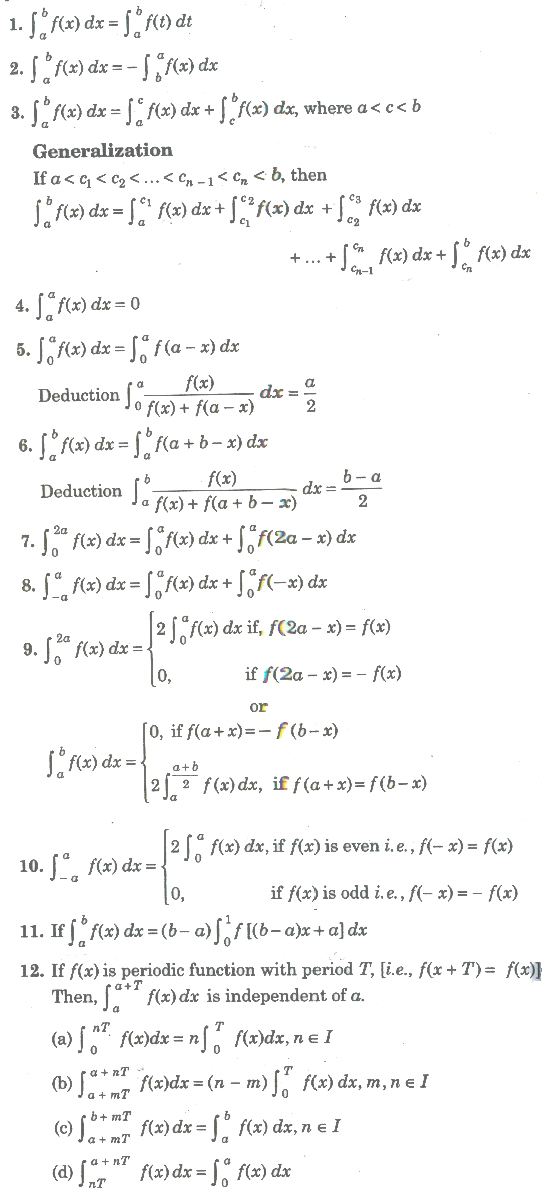
13. Leibnitz Rule for Differentiation Under Integral Sign
(a) If Φ(x) and ψ(x) are defined on [a, b] and differentiable for every x and f(t) is continuous, then
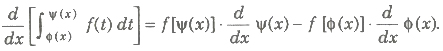
(b) If Φ(x) and ψ(x) are defined on [a, b] and differentiable for every x and f(t) is continuous, then
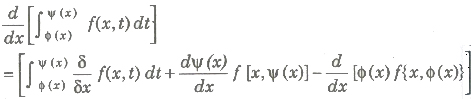

14. If f(x) ≥ 0 on the interval [a, b], then
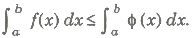
15. If (x) ≤ Φ(x) for x ∈ [a, b], then
16. If at every point x of an interval [a, b] the inequalities
g(x) ≤ f(x) ≤ h(x)

are fulfilled, then

18. If m is the least value and M is the greatest value of the function f(x) on the interval [a, bl. (estimation of an integral), then
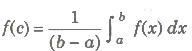
19. If f is continuous on [a, b], then there exists a number c in [a, b] at which
is called the mean value of the function f(x) on the interval [a, b].
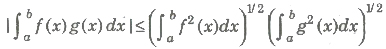
20. If f22 (x) and g2 (x) are integrable on [a, b], then
21. Let a function f(x, α) be continuous for a ≤ x ≤ b and c ≤ α ≤ d.
Then, for any α ∈ [c, d], if
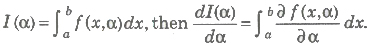
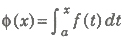
22. If f(t) is an odd function, then is an even function.
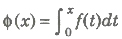
23. If f(t) is an even function, then is an odd function.

24. If f(t) is an even function, then for non-zero a, is not necessarily an odd function. It will be an odd function, if
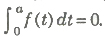
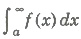
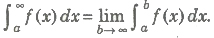
25. If f(x) is continuous on [a, α], then is called an improper integral and is defined as
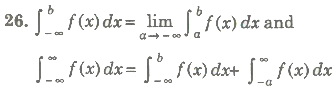

27. Geometrically, for f(x) > 0, the improper integral gives area of the figure bounded by the curve y = f(x), the axis and the straight line x = a.
Integral Function
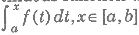
Let f(x) be a continuous function defined on [a, b], then a function φ(x) defined by is called the integral function of the function f.
Properties of Integral Function
- The integral function of an integrable function is continuous.
- If φ(x) is the integral function of continuous function, then φ(x) is derivable and of φ ‘ = f(x) for all x ∈ [a, b].
Gamma Function
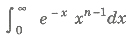
If n is a positive rational number, then the improper integral is defined as a gamma function and it is denoted by Γn
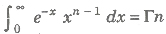
Properties of Gamma Function
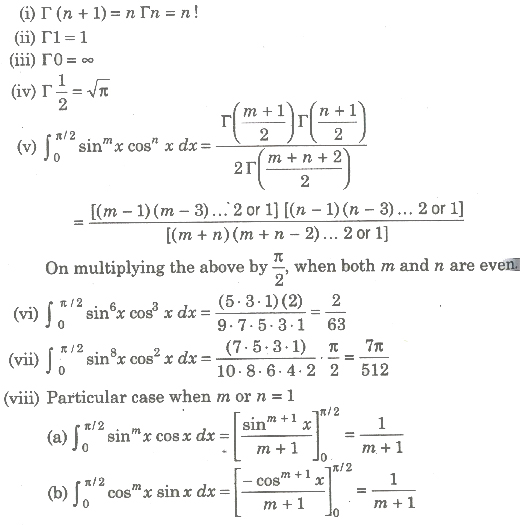
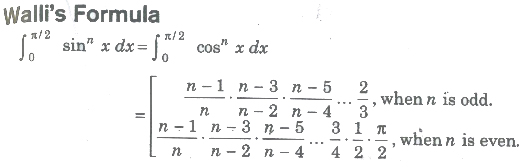
Summation of Series by Definite Integral

The method to evaluate the integral, as limit of the sum of an infinite series is known as integration by first principle.
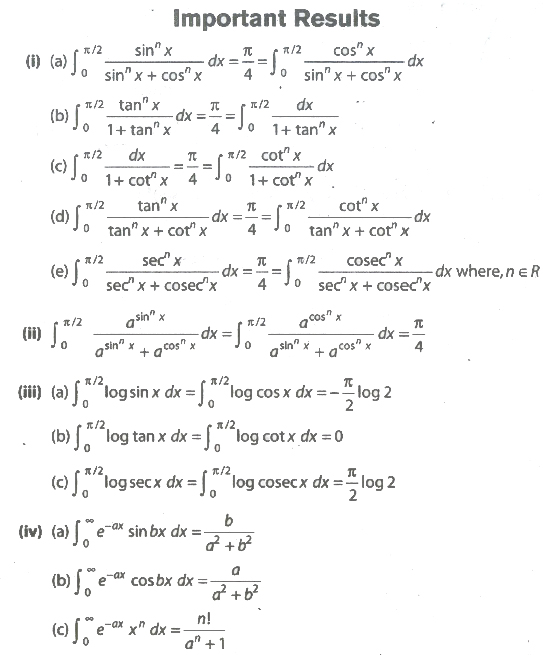
Area of Bounded Region
The space occupied by the curve along with the axis, under the given condition is called area of bounded region.
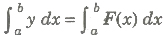
(i) The area bounded by the curve y = F(x) above the X-axis and between the lines x = a, x = b is given by

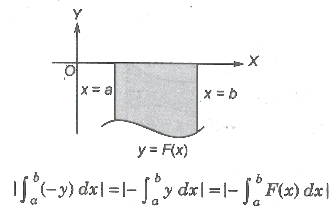
(ii) If the curve between the lines x = a, x = b lies below the X-axis, then the required area is given by
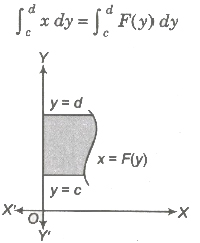
(iii) The area bounded by the curve x = F(y) right to the Y-axis and the lines y = c, y = d is given by
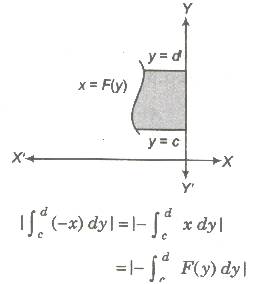
(iv) If the curve between the lines y = c, y = d left to the Y-axis, then the area is given by

(v) Area bounded by two curves y = F (x) and y = G (x) between x = a and x = b is given by
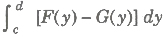
(vi) Area bounded by two curves x = f(y) and x = g(y) between y=c and y=d is given by
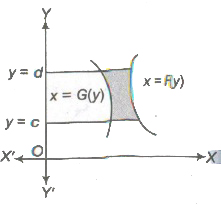
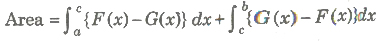
(vii) If F (x) ≥. G (x) in [a, c] and F (x) ≤ G (x) in [c,d], where a < c < b, then area of the region bounded by the curves is given as
Area of Curves Given by Polar Equations
Let f(θ) be a continuous function, θ ∈ (a, α), then the are t bounded by the curve r = f(θ) and radius α, β(α < β) is
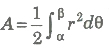
Area of Parametric Curves
Let x = φ(t) and y = ψ(t) be two parametric curves, then area bounded by the curve, X-axis and ordinates x = φ(t1), x = ψ(t2) is

Volume and Surface Area
If We revolve any plane curve along any line, then solid so generated is called solid of revolution.
1. Volume of Solid Revolution
- The volume of the solid generated by revolution of the area bounded by the curve y = f(x), the axis of x and the ordinates it being given that f(x) is a continuous a function in the interval (a, b).
- The volume of the solid generated by revolution of the area bounded by the curve x = g(y), the axis of y and two abscissas y = c and y = d is it being given that g(y) is a continuous function in the interval (c, d).
Surface of Solid Revolution
(i) The surface of the solid generated by revolution of the area bounded by the curve y = f(x), the axis of x and the ordinates

is a continuous function in the interval (a, b).
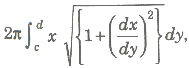
(ii) The surface of the solid generated by revolution of the area bounded by the curve x = f (y), the axis of y and y = c, y = d is continuous function in the interval (c, d).
Curve Sketching
1. symmetry
- If powers of y in a equation of curve are all even, then curve is symmetrical about X-axis.
- If powers of x in a equation of curve are all even, then curve is symmetrical about Y-axis.
- When x is replaced by -x and y is replaced by -y, then curve is symmetrical in opposite quadrant.
- If x and y are interchanged and equation of curve remains unchanged curve is symmetrical about line y = x.
2. Nature of Origin
- If point (0, 0) satisfies the equation, then curve passes through origin.
- If curve passes through origin, then equate low st degree term to zero and get equation of tangent. If there are two tangents, then origin is a double point.
3. Point of Intersection with Axes
- Put y = 0 and get intersection with X-axis, put x = 0 and get intersection with Y-axis.
- Now, find equation of tangent at this point i. e. , shift origin to the point of intersection and equate the lowest degree term to zero.
- Find regions where curve does not exists. i. e., curve will not exit for those values of variable when makes the other imaginary or not defined.
4. Asymptotes
- Equate coefficient of highest power of x and get asymptote parallel to X-axis.
- Similarly equate coefficient of highest power of y and get asymptote parallel to Y-axis.
5. The Sign of (dy/dx)
Find points at which (dy/dx) vanishes or becomes infinite. It gives us the points where tangent is parallel or perpendicular to the X-axis.
6. Points of Inflexion
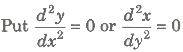
and solve the resulting equation.If some point of inflexion is there, then locate it exactly.
Taking in consideration of all above information, we draw an approximate shape of the curve.
Shape of Some Curves is Given Below

Class 12 Key Points, Important Questions & Practice Papers
Hope these notes helped you in your schools exam preparation. Candidates can also check out the Key Points, Important Questions & Practice Papers for various Subjects for Class 12 in both Hindi and English language form the link below.
Class 12 NCERT Solutions
Candidates who are studying in Class 12 can also check Class 12 NCERT Solutions from here. This will help the candidates to know the solutions for all subjects covered in Class 12th. Candidates can click on the subject wise link to get the same. Class 12 Chapter-wise, detailed solutions to the questions of the NCERT textbooks are provided with the objective of helping students compare their answers with the sample answers.
Class 12 Mock Test / Practice
Mock test are the practice test or you can say the blue print of the main exam. Before appearing in the main examination, candidates must try mock test as it helps the students learn from their mistakes. With the help of Class 12 Mock Test / Practice, candidates can also get an idea about the pattern and marking scheme of that examination. For the sake of the candidates we are providing Class 12 Mock Test / Practice links below.
Class 12 Exemplar Questions
Exemplar Questions Class 12 is a very important resource for students preparing for the Examination. Here we have provided Exemplar Problems Solutions along with NCERT Exemplar Problems Class 12. Question from very important topics is covered by Exemplar Questions for Class 12.
Class 12 Maths
Chemistry Notes Physics Notes Biology Notes
To get study material, exam alerts and news, join our Whatsapp Channel.




