Class 12 Maths Three Dimensional Geometry – Get here the Notes for Class 12 Maths Three Dimensional Geometry. Candidates who are ambitious to qualify the Class 12 with good score can check this article for Notes. This is possible only when you have the best CBSE Class 12 Maths study material and a smart preparation plan. To assist you with that, we are here with notes. Hope these notes will helps you understand the important topics and remember the key points for exam point of view. Below we provided the Notes of Class 12 Maths for topic Three Dimensional Geometry.
- Class: 12th
- Subject: Maths
- Topic: Three Dimensional Geometry
- Resource: Notes
CBSE Notes Class 12 Maths Three Dimensional Geometry
Candidates who are pursuing in Class 12 are advised to revise the notes from this post. With the help of Notes, candidates can plan their Strategy for particular weaker section of the subject and study hard. So, go ahead and check the Important Notes for Class 12 Maths Three Dimensional Geometry
Coordinate System
The three mutually perpendicular lines in a space which divides the space into eight parts and if these perpendicular lines are the coordinate axes, then it is said to be a coordinate system.
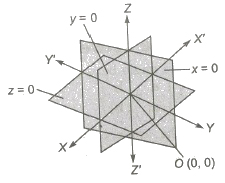
Sign Convention

Distance between Two Points
Let P(x1, y1, z1) and Q(x2, y2, z2) be two given points. The distance between these points is given by
PQ √(x2 – x1)2 + (y2 – y1)2 + (z2 – z1)2
The distance of a point P(x, y, z) from origin O is
OP = √x2 + y2 + z2
Section Formulae
(i) The coordinates of any point, which divides the join of points P(x1, y1, z1) and Q(x2, y2, z2) in the ratio m : n internally are
(mx2 + nx1 / m + n, my2 + ny1 / m + n, mz2 + nz1 / m + n)
(ii) The coordinates of any point, which divides the join of points P(x1, y1, z1) and Q(x2, y2, z2) in the ratio m : n externally are
(mx2 – nx1 / m – n, my2 – ny1 / m – n, mz2 – nz1 / m – n)
(iii) The coordinates of mid-point of P and Q are
(x1 + x2 / 2 , y1 + y2 / 2, z1 + z2 / 2)
(iv) Coordinates of the centroid of a triangle formed with vertices P(x1, y1, z1) and Q(x2, y2, z2) and R(x3, y3, z3) are
(x1 + x2 + x3 / 3 , y1 + y2 + y3 / 3, z1 + z2 + z3 / 3)
(v) Centroid of a Tetrahedron
If (x1, y1, z1), (x2, y2, z2), (x3, y3, z3) and (x4, y4, z4) are the vertices of a tetrahedron, then its centroid G is given by
(x1 + x2 + x3 + x4 / 4 , y1 + y2 + y3 + y4 / 4, z1 + z2 + z3 + z4 / 4)
Direction Cosines
If a directed line segment OP makes angle α, β and γ with OX , OY and OZ respectively, then Cos α, cos β and cos γ are called direction cosines of up and it is represented by l, m, n.
i.e.,
l = cos α
m = cos β
and n = cos γ
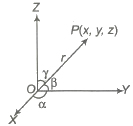
If OP = r, then coordinates of OP are (lr, mr , nr)
(i) If 1, m, n are direction cosines of a vector r, then
(a) r = |r| (li + mj + nk) ⇒ r = li + mj + nk
(b) l2 + m2 + n2 = 1
(c) Projections of r on the coordinate axes are
(d) |r| = l|r|, m|r|, n|r| / √sum of the squares of projections of r on the coordinate axes
(ii) If P(x1, y1, z1) and Q(x2, y2, z2) are two points, such that the direction cosines of PQ are l, m, n. Then,
x2 – x1 = l|PQ|, y2 – y1 = m|PQ|, z2 – z1 = n|PQ|
These are projections of PQ on X , Y and Z axes, respectively.
(iii) If 1, m, n are direction cosines of a vector r and a b, c are three numbers, such that l / a = m / b = n / c.
Then, we say that the direction ratio of r are proportional to a, b, c.
Also, we have
l = a / √a2 + b2 + c2, m = b / √a2 + b2 + c2, n = c / √a2 + b2 + c2
(iv) If θ is the angle between two lines having direction cosines l1, m1, n1 and 12, m2, n2, then
cos θ = l112 + m1m2 + n1n2
(a) Lines are parallel, if l1 / 12 = m1 / m2 = n1 / n2
(b) Lines are perpendicular, if l112 + m1m2 + n1n2
(v) If θ is the angle between two lines whose direction ratios are proportional to a1, b1, c1 and a2, b2, c2 respectively, then the angle θ between them is given by
cos θ = a1a2 + b1b2 + c1c2 / √a21 + b21 + c21 √a22 + b22 + c22
Lines are parallel, if a1 / a2 = b1 / b2 = c1 / c2
Lines are perpendicular, if a1a2 + b1b2 + c1c2 = 0.
(vi) The projection of the line segment joining points P(x1, y1, z1) and Q(x2, y2, z2) to the line having direction cosines 1, m, n is
|(x2 – x1)l + (y2 – y1)m + (z2 – z1)n|.
(vii) The direction ratio of the line passing through points P(x1, y1, z1) and Q(x2, y2, z2) are proportional to x2 – x1, y2 – y1 – z2 – z1 Then, direction cosines of PQ are
x2 – x1 / |PQ|, y2 – y1 / |PQ|, z2 – z1 / |PQ|
Area of Triangle
If the vertices of a triangle be A(x1, y1, z1) and B(x2, y2, z2) and C(x3, y3, z3), then
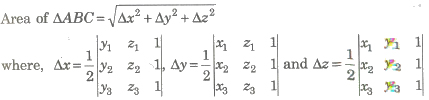
Angle Between Two Intersecting Lines
If l(x1, m1, n1) and l(x2, m2, n2) be the direction cosines of two given lines, then the angle θ between them is given by
cos θ = l112 + m1m2 + n1n2
(i) The angle between any two diagonals of a cube is cos-1 (1 / 3).
(ii) The angle between a diagonal of a cube and the diagonal of a face (of the cube is cos-1 (√2 / 3)
Straight Line in Space
The two equations of the line ax + by + cz + d = 0 and a’ x + b’ y + c’ z + d’ = 0 together represents a straight line.
1. Equation of a straight line passing through a fixed point A(x1, y1, z1) and having direction ratios a, b, c is given by
x – x1 / a = y – y1 / b = z – z1 / c, it is also called the symmetrically form of a line.
Any point P on this line may be taken as (x1 + λa, y1 + λb, z1 + λc), where λ ∈ R is parameter. If a, b, c are replaced by direction cosines 1, m, n, then λ, represents distance of the point P from the fixed point A.
2. Equation of a straight line joining two fixed points A(x1, y1, z1) and B(x2, y2, z2) is given by
x – x1 / x2 – x1 = y – y1 / y2 – y1 = z – z1 / z2 – z1
3. Vector equation of a line passing through a point with position vector a and parallel to vector b is r = a + λ b, where A, is a parameter.
4. Vector equation of a line passing through two given points having position vectors a and b is r = a + λ (b – a) , where λ is a parameter.
5. (a) The length of the perpendicular from a point on the line r – a + λ b is given by
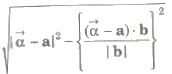
(b) The length of the perpendicular from a point P(x1, y1, z1) on the line
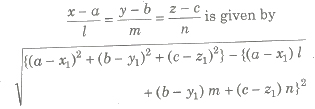
where, 1, m, n are direction cosines of the line.
6. Skew Lines Two straight lines in space are said to be skew lines, if they are neither parallel nor intersecting.
7. Shortest Distance If l1 and l2 are two skew lines, then a line perpendicular to each of lines 4 and 12 is known as the line of shortest distance.
If the line of shortest distance intersects the lines l1 and l2 at P and Q respectively, then the distance PQ between points P and Q is known as the shortest distance between l1 and l2.
8. The shortest distance between the lines
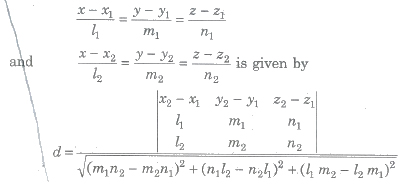
9. The shortest distance between lines r = a1 + λb1 and r = a2 + μb2 is given by
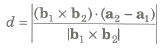
10. The shortest distance parallel lines r = a1 + λb1 and r = a2 + μb2 is given by

11. Lines r = a1 + λb1 and r = a2 + μb2 are intersecting lines, if (b1 * b2) * (a2 – a1) = 0.
12. The image or reflection (x, y, z) of a point (x1, y1, z1) in a plane ax + by + cz + d = 0 is given by
x – x1 / a = y – y1 / b = z – z1 / c = – 2 (ax1 + by1 + cz1 + d) / a2 + b2 + c2
13. The foot (x, y, z) of a point (x1, y1, z1) in a plane ax + by + cz + d = 0 is given by
x – x1 / a = y – y1 / b = z – z1 / c = – (ax1 + by1 + cz1 + d) / a2 + b2 + c2
14. Since, x, y and z-axes pass through the origin and have direction cosines (1, 0, 0), (0, 1, 0) and (0, 0, 1), respectively. Therefore, their equations are
x – axis : x – 0 / 1 = y – 0 / 0 = z – 0 / 0
y – axis : x – 0 / 0 = y – 0 / 1 = z – 0 / 0
z – axis : x – 0 / 0 = y – 0 / 0 = z – 0 / 1
Plane
A plane is a surface such that, if two points are taken on it, a straight line joining them lies wholly in the surface.
General Equation of the Plane
The general equation of the first degree in x, y, z always represents a plane. Hence, the general equation of the plane is ax + by + cz + d = 0. The coefficient of x, y and z in the cartesian equation of a plane are the direction ratios of normal to the plane.
Equation of the Plane Passing Through a Fixed Point
The equation of a plane passing through a given point (x1, y1, z1) is given by a(x – x1) + b (y — y1) + c (z — z1) = 0.
Normal Form of the Equation of Plane
(i) The equation of a plane, which is at a distance p from origin and the direction cosines of the normal from the origin to the plane are l, m, n is given by lx + my + nz = p.
(ii) The coordinates of foot of perpendicular N from the origin on the plane are (1p, mp, np).

Intercept Form
The intercept form of equation of plane represented in the form of
x / a + y / b + z / c = 1
where, a, b and c are intercepts on X, Y and Z-axes, respectively.
For x intercept Put y = 0, z = 0 in the equation of the plane and obtain the value of x. Similarly, we can determine for other intercepts.
Equation of Planes with Given Conditions
(i) Equation of a plane passing through the point A(x1, y1, z1) and parallel to two given lines with direction ratios
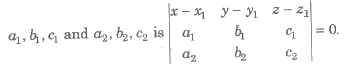
(ii) Equation of a plane through two points A(x1, y1, z1) and B(x2, y2, z2) and parallel to a line with direction ratios a, b, c is
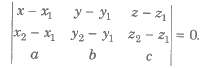
(iii) The Equation of a plane passing through three points A(x1, y1, z1), B(x2, y2, z2) and C(x3, y3, z3) is
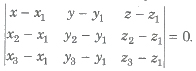
(iv) Four points A(x1, y1, z1), B(x2, y2, z2), C(x3, y3, z3) and D(x4, y4, z4) are coplanar if and only if

(v) Equation of the plane containing two coplanar lines
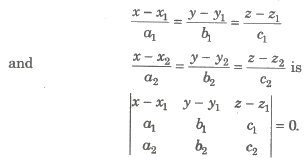
Angle between Two Planes
The angle between two planes is defined as the angle between the normal to them from any point.
Thus, the angle between the two planes
a1x + b1y + c1z + d1 = 0
and a2x + b2y + c2z + d2 = 0
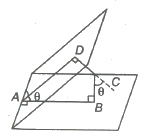
is equal to the angle between the normals with direction cosines
± a1 / √Σ a21, ± b1 / √Σ a21, ± c1 / √Σ a21
and ± a2 / √Σ a22, ± b2 / √Σ a22, ± c2 / √Σ a22
If θ is the angle between the normals, then
cos θ = ± a1a2 + b1b2 + c1c2 / √a21 + b21 + c21 √a22 + b22 + c22
Parallelism and Perpendicularity of Two Planes
Two planes are parallel or perpendicular according as the normals to them are parallel or perpendicular.
Hence, the planes a1x + b1y + c1z + d1 = 0 and a2x + b2y + c2z + d2 = 0
are parallel, if a1 / a2 = b1 / b2 = c1 / c2 and perpendicular, if a1a2 + b1b2 + c1c2 = 0.
Note The equation of plane parallel to a given plane ax + by + cz + d = 0 is given by ax + by + cz + k = 0, where k may be determined from given conditions.
Angle between a Line and a Plane
In Vector Form The angle between a line r = a + λ b and plane r *• n = d, is defined as the complement of the angle between the line and normal to the plane:
sin θ = n * b / |n||b|
In Cartesian Form The angle between a line x – x1 / a1 = y – y1 / b1 = z – z1 / c1
and plane a2x + b2y + c2z + d2 = 0 is sin θ = a1a2 + b1b2 + c1c2 / √a21 + b21 + c21 √a22 + b22 + c22
Distance of a Point from a Plane
Let the plane in the general form be ax + by + cz + d = 0. The distance of the point P(x1, y1, z1) from the plane is equal to

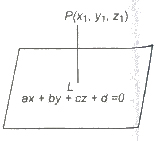
If the plane is given in, normal form lx + my + nz = p. Then, the distance of the point P(x1, y1, z1) from the plane is |lx1 + my1 + nz1 – p|.
Distance between Two Parallel Planes
If ax + by + cz + d1 = 0 and ax + by + cz + d2 = 0 be equation of two parallel planes. Then, the distance between them is

Bisectors of Angles between Two Planes
The bisector planes of the angles between the planes
a1x + b1y + c1z + d1 = 0, a2x + b2y + c2z + d2 = 0 is
a1x + b1y + c1z + d1 / √Σa21 = ± a2x + b2y + c2z + d2 / √Σa22
One of these planes will bisect the acute angle and the other obtuse angle between the given plane.
Sphere
A sphere is the locus of a point which moves in a space in such a way that its distance from a fixed point always remains constant.
General Equation of the Sphere
In Cartesian Form The equation of the sphere with centre (a, b, c) and radius r is
(x – a)2 + (y – b)2 + (z – c)2 = r2 …….(i)
In generally, we can write
x2 + y2 + z2 + 2ux + 2vy + 2wz + d = 0
Here, its centre is (-u, v, w) and radius = √u2 + v2 + w2 – d
In Vector Form The vector equation of a sphere of radius a and Centre having position vector c is |r – c| = a
Important Points to be Remembered
(i) The general equation of second degree in x, y, z is ax2 + by2 + cz2 + 2hxy + 2kyz + 2lzx + 2ux + 2vy + 2wz + d = 0
represents a sphere, if
(a) a = b = c (≠ 0)
(b) h = k = 1 = 0
The equation becomes
ax2 + ay2 + az2 + 2ux + 2vy + 2wz + d – 0 …(A)
To find its centre and radius first we make the coefficients of x2, y2 and z2 each unity by dividing throughout by a.
Thus, we have
x2+y2+z2 + (2u / a) x + (2v / a) y + (2w / a) z + d / a = 0 …..(B)
∴ Centre is (- u / a, – v / a, – w / a)
and radius = √u2 / a2 + v2 / a2 + w2 / a2 – d / a
= √u2 + v2 + w2 – ad / |a| .
(ii) Any sphere concentric with the sphere
x2 + y2 + z2 + 2ux + 2vy + 2wz + d = 0
is x2 + y2 + z2 + 2ux + 2vy + 2wz + k = 0
(iii) Since, r2 = u2 + v2 + w2 — d, therefore, the Eq. (B) represents a real sphere, if u2 +v2 + w2 — d > 0
(iv) The equation of a sphere on the line joining two points (x1, y1, z1) and (x2, y2, z2) as a diameter is
(x – x1) (x – x1) + (y – y1) (y – y2) + (z – z1) (z – z2) = 0.
(v) The equation of a sphere passing through four non-coplanar points (x1, y1, z1), (x2, y2, z2), (x3, y3, z3) and (x4, y4, z4) is

Tangency of a Plane to a Sphere
The plane lx + my + nz = p will touch the sphere x2 + y2 + z2 + 2ux + 2vy + 2 wz + d = 0, if length of the perpendicular from the centre ( – u, – v,— w)= radius,
i.e., |lu – mv – nw – p| / √l2 + m2 + n2 = √u2 + v2 + w2 – d
(lu – mv – nw – p)2 = (u2 + v2 + w2 – d) (l2 + m2 + n2)
Plane Section of a Sphere
Consider a sphere intersected by a plane. The set of points common to both sphere and plane is called a plane section of a sphere.
In ΔCNP, NP2 = CP2 – CN2 = r2 – p2
∴ NP = √r2 – p2

Hence, the locus of P is a circle whose centre is at the point N, the foot of the perpendicular from the centre of the sphere to the plane.
The section of sphere by a plane through its centre is called a great circle. The centre and radius of a great circle are the same as those of the sphere.
Class 12 Key Points, Important Questions & Practice Papers
Hope these notes helped you in your schools exam preparation. Candidates can also check out the Key Points, Important Questions & Practice Papers for various Subjects for Class 12 in both Hindi and English language form the link below.
Class 12 NCERT Solutions
Candidates who are studying in Class 12 can also check Class 12 NCERT Solutions from here. This will help the candidates to know the solutions for all subjects covered in Class 12th. Candidates can click on the subject wise link to get the same. Class 12 Chapter-wise, detailed solutions to the questions of the NCERT textbooks are provided with the objective of helping students compare their answers with the sample answers.
Class 12 Mock Test / Practice
Mock test are the practice test or you can say the blue print of the main exam. Before appearing in the main examination, candidates must try mock test as it helps the students learn from their mistakes. With the help of Class 12 Mock Test / Practice, candidates can also get an idea about the pattern and marking scheme of that examination. For the sake of the candidates we are providing Class 12 Mock Test / Practice links below.
Class 12 Exemplar Questions
Exemplar Questions Class 12 is a very important resource for students preparing for the Examination. Here we have provided Exemplar Problems Solutions along with NCERT Exemplar Problems Class 12. Question from very important topics is covered by Exemplar Questions for Class 12.
Class 12 Maths
Chemistry Notes Physics Notes Biology Notes
To get study material, exam alerts and news, join our Whatsapp Channel.



