Logic
Logic is the subject that deals with the method of reasoning. It provides us rules for determining the validity of a given argument in proving theorem.
Statement (Proposition)
A statement is an assertive sentence which is either true or false but not both a true statement is called valid statement. Otherwise it is called invalid statement. Statements are denoted by the small letters
i.e., p, q, r … etc.
Open and Compound Statement
A sentence which contains one or more variable such that when certain values are given to the variable it becomes a statement, is called an open statement.
If two or more simple statements are combined by the use of words such as ‘and’, ‘or’, ‘not’, ‘if’, ‘then’, ‘if and only if ‘, then the resulting statement is called a compound statement.
Truth Value and Truth Table
A statement can be either ‘true’ or ‘false’ which are called truth values of a .statement and it is represented by the symbols T and F, respectively.
A. truth table is a summary of truth values of the resulting statements for all possible assignment of values to the variables appearing in a compound statement.
Number of rows depends on their number of statements.
Truth Table for Two Statements (p, q)
Number of rows = 22 = 4
| p | q |
| T | T |
| T | F |
| F | T |
| F | F |
Elementary Operation of Logic
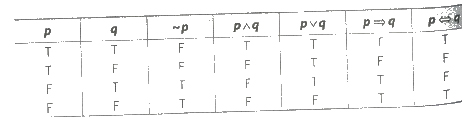
(i) Conjunction A compound sentence formed by two simple sentences p and q using connective ‘and’ is called the conjunction of p and q and it is represented by p ∧ q.
(ii) Disjunction A compound sentence formed by two simple sentences p and q using connectives ‘or’ is called the disjunction of p and q and it is represented by p ∨ q.
(iii) Negation A statement which is formed by changing the truth value of a given statement by using the word like ‘no’, ‘not’ is called negation of given statement. If p is a statement, then negation of p is denoted by ~ p.
(iv) Conditional Sentence (Implication) Two simple sentences p and q connected by the phase, if and then, is called conditional sentence of p and q arid it is denoted by p => q.
(v) Biconditional Sentence (Bi-implication) The two simple sentences connected by the phrase, ‘if and only if this is called biconditional sentences. It is denoted by the symbol ‘<=>’.
Table for Basic Logical Connections
Tautology and Contradiction
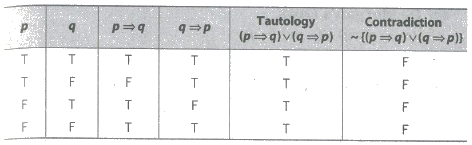
The compound statement which are true for every value of their components are called tautology.
The compound statements which are false for every value of their components are called contradiction (fallacy).
Truth Table
Quantifiers and Quantified Statements
In this statements, there are two important symbols are used.
(i) The symbol ‘∀’ stands for ‘all values of ‘.
This is known as universal quantifier.
(ii) The symbol ‘∃’ stands for ‘there exists’.
The symbol ∃ is known as existential quantifier.
Quantified Statement
An open sentence with a quantifier becomes a statement, called a quantified statement.
Negation of a Quantified Statement
(i) ~{∀ x ∈ A : p(x) is true} = {∃ x ∈ A such that (s.t.) ~ p(x) is true}
(ii) ~{∃x ∈ A : p(x) is true} = {∀ x ∈ A : ~ p(x) is true}
Laws of Algebra of Statements
(i) Idempotent Laws
(a) p ∨ p ≡ p
(b) p ∧ p ≡ p
(ii) Associative Laws
(a) (p ∨ q) ∨ r ≡ p ∨ (q ∨ r)
(b) (p ∧ q) ∧ r ≡ p ∧ (q ∧ r)
(iii) Commutative Laws
(a) p ∨ q ≡ q ∨ p
(b) p ∧ q ≡ q ∧ P
(iv) Distributive Laws
(a) p ∨ (q A r) ≡ (p ∨ q) ∧ (p ∨ r)
(b) p ∧ (q ∨ r) ≡ (p ∧ q) ∨ (p ∧ r)
(v) De Morgan’s Laws
(a) ~(p ∨ q) ≡ (~ p) ∧ (,_ q)
(b) ~(p ∧ q) ≡ (~ p) ∨ (~ q)
(vi) Identity Laws
(a) p ∧ F ≡ F
(b) p ∧ T ≡ p
(c) p ∨ T ≡ T
(d) p ∨ F ≡ p
(vii) Complement Laws
(a) p ∨ (~ p) ≡ T
(b) p ∧ (~ p) ≡ F
(c) ~ (~p) ≡ p
(d) ~ T ≡ F, ~ F ≡ T
Important Points to be Remembered
(i) The number of rows of table is depend on the number of statements.
(a) If p is false, then ~ p is true.
(b) If P is true, then ~ p is false.
(ii) (a) The converse of p => q is q => p.
(b) The inverse of p => q is ~ p => ~ q.
(iii) The contrapositive of p => q is ~ q => ~ p.
A statement which is neither a tautology nor a contradiction is a contingency.
| « Click Here for Previous Topic | Click Here for Next Topic » |
Click Here for CBSE Class 11 Maths All Chapters Notes
To get fastest exam alerts and government job alerts in India, join our Telegram channel.
Discussion about this post