Class 12 Maths Determinant – Get here the Notes for Class 12 Maths Determinant. Candidates who are ambitious to qualify the Class 12 with good score can check this article for Notes. This is possible only when you have the best CBSE Class 12 Maths study material and a smart preparation plan. To assist you with that, we are here with notes. Hope these notes will helps you understand the important topics and remember the key points for exam point of view. Below we provided the Notes of Class 12 Maths for topic Determinant.
- Class: 12th
- Subject: Maths
- Topic: Determinant
- Resource: Notes
CBSE Notes Class 12 Maths Determinant
Candidates who are pursuing in Class 12 are advised to revise the notes from this post. With the help of Notes, candidates can plan their Strategy for particular weaker section of the subject and study hard. So, go ahead and check the Important Notes for Class 12 Maths Determinant
Determinant
Every square matrix A is associated with a number, called its determinant and it is denoted by det (A) or |A| .
Only square matrices have determinants. The matrices which are not square do not have determinants
(i) First Order Determinant
If A = [a], then det (A) = |A| = a
(ii) Second Order Determinant
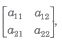
|A| = a11a22 – a21a12
(iii) Third Order Determinant
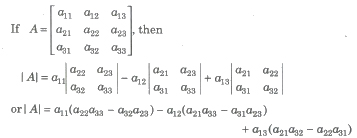
Evaluation of Determinant of Square Matrix of Order 3 by Sarrus Rule
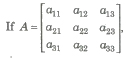
then determinant can be formed by enlarging the matrix by adjoining the first two columns on the right and draw lines as show below parallel and perpendicular to the diagonal.
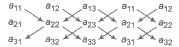
The value of the determinant, thus will be the sum of the product of element. in line parallel to the diagonal minus the sum of the product of elements in line perpendicular to the line segment. Thus,
Δ = a11a22a33 + a12a23a31 + a13a21a32 – a13a22a31 – a11a23a32 – a12a21a33.
Note This method doesn’t work for determinants of order greater than 3.
Properties of Determinants
(i) The value of the determinant remains unchanged, if rows are changed into columns and columns are changed into rows e.g.,
|A’| = |A|
(ii) If A = [aij]n x n , n > 1 and B be the matrix obtained from A by interchanging two of its rows or columns, then
det (B) = – det (A)
(iii) If two rows (or columns) of a square matrix A are proportional, then |A| = O.
(iv) |B| = k |A| ,where B is the matrix obtained from A, by multiplying one row (or column) of A by k.
(v) |kA| = kn|A|, where A is a matrix of order n x n.
(vi) If each element of a row (or column) of a determinant is the sum of two or more terms, then the determinant can be expressed as the sum of two or more determinants, e.g.,
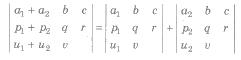
(vii) If the same multiple of the elements of any row (or column) of a determinant are added to the corresponding elements of any other row (or column), then the value of the new determinant remains unchanged, e.g.,

(viii) If each element of a row (or column) of a determinant is zero, then its value is zero.
(ix) If any two rows (columns) of a determinant are identical, then its value is zero.
(x) If each element of row (column) of a determinant is expressed as a sum of two or more terms, then the determinant can be expressed as the sum of two or more determinants.
Important Results on Determinants
(i) |AB| = |A||B| , where A and B are square matrices of the same order.
(ii) |An| = |A|n
(iii) If A, B and C are square matrices of the same order such that ith column (or row) of A is the sum of i th columns (or rows) of B and C and all other columns (or rows) of A, Band C are identical, then |A| =|B| + |C|
(iv) |In| = 1,where In is identity matrix of order n
(v) |On| = 0, where On is a zero matrix of order n
(vi) If Δ(x) be a 3rd order determinant having polynomials as its elements.
(a) If Δ(a) has 2 rows (or columns) proportional, then (x – a) is a factor of Δ(x).
(b) If Δ(a) has 3 rows (or columns) proportional, then (x – a)2 is a factor of Δ(x). ,
(vii) A square matrix A is non-singular, if |A| ≠ 0 and singular, if |A| =0.
(viii) Determinant of a skew-symmetric matrix of odd order is zero and of even order is a non-zero perfect square.
(ix) In general, |B + C| ≠ |B| + |C|
(x) Determinant of a diagonal matrix = Product of its diagonal elements
(xi) Determinant of a triangular matrix = Product of its diagonal elements
(xii) A square matrix of order n, is non-singular, if its rank r = n i.e., if |A| ≠ 0, then rank (A) = n
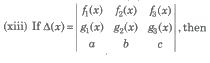
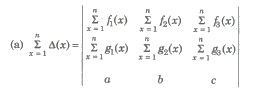
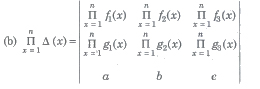
(xiv) If A is a non-singular matrix, then |A-1| = 1 / |A| = |A|-1
(xv) Determinant of a orthogonal matrix = 1 or – 1.
(xvi) Determinant of a hermitian matrix is purely real .
(xvii) If A and B are non-zero matrices and AB = 0, then it implies |A| = 0 and |B| = 0.
Minors and Cofactors
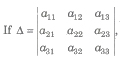
then the minor Mij of the element aij is the determinant obtained by deleting the i row and jth column.
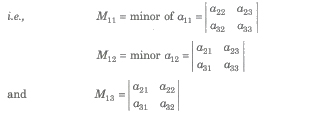
The cofactor of the element aij is Cij = (- 1)i + j Mij
Adjoint of a Matrix – Adjoint of a matrix is the transpose of the matrix of cofactors of the give matrix, i.e.,
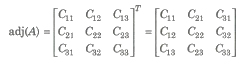
Properties of Minors and Cofactors
(i) The sum of the products of elements of .any row (or column) of a determinant with the cofactors of the corresponding elements of any other row (or column) is zero, i.e., if

then a11C31 + a12C32 + a13C33 = 0 ans so on.
(ii) The sum of the product of elements of any row (or column) of a determinant with the cofactors of the corresponding elements of the same row (or column) is Δ


Differentiation of Determinant
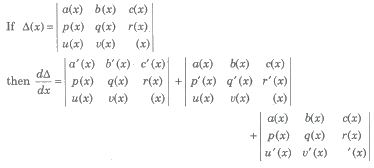
Integration of Determinant
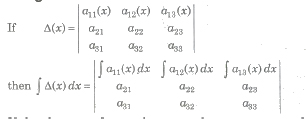
If the elements of more than one column or rows are functions of x, then the integration can be done only after evaluation/expansion of the determinant.
Solution of Linear equations by Determinant/Cramer’s Rule
Case 1. The solution of the system of simultaneous linear equations
a1x + b1y = C1 …(i)
a2x + b2y = C2 …(ii)
is given by x = D1 / D, Y = D2 / D
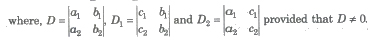
(i) If D ≠ 0, then the given system of equations is consistent and has a unique solution given by x = D1 / D, y = D2 / D
(ii) If D = 0 and Dl = D2 = 0, then the system is consistent and has infinitely many solutions.
(iii) If D = 0 and one of Dl and D2 is non-zero, then the system is inconsistent.
Case II. Let the system of equations be
a1x + b1y + C1z = d1
a2x + b2y + C2z = d2
a3x + b3y + C3z = d3
Then, the solution of the system of equation is
x = D1 / D, Y = D2 / D, Z = D3 / D, it is called Cramer’s rule.
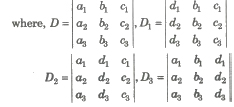
(i) If D ≠ 0, then the system of equations is consistent with unique solution.
(ii) If D = 0 and atleast one of the determinant D1, D2, D3 is non-zero, then the given system is inconsistent, i.e., having no solution.
(iii) If D = 0 and D1 = D2 = D3 = 0, then the system is consistent, with infinitely many solutions.
(iv) If D ≠ 0 and D1 = D2 = D3 = 0, then system has only trivial solution, (x = y = z = 0).
Cayley-Hamilton Theorem
Every matrix satisfies its characteristic equation, i.e., if A be a square matrix, then |A – xl| = 0 is the characteristics equation of A. The values of x are called eigenvalues of A.
i.e., if x3 – 4x2 – 5x – 7 = 0 is characteristic equation for A, then
A3 – 4A2 + 5A – 7I = 0
Properties of Characteristic Equation
(i) The sum of the eigenvalues of A is equal to its trace.
(ii) The product of the eigenvalues of A is equal to its determinant.
(iii) The eigenvalues of an orthogonal matrix are of unit modulus.
(iv) The feigen values of a unitary matrix are of unit modulus.
(v) A and A’ have same eigenvalues.
(vi) The eigenvalues of a skew-hermitian matrix are either purely imaginary or zero.
(vii) If x is an eigenvalue of A, then x is the eigenvalue of A* .
(viii) The eigenvalues of a triangular matrix are its diagonal elements.
(ix) If x is the eigenvalue of A and |A| ≠ 0, then (1 / x) is the eigenvalue of A-1.
(x) If x is the eigenvalue of A and |A| ≠ 0, then |A| / x is the eigenvalue of adj (A).
(xi) If x1, x2,x3, … ,xn are eigenvalues of A, then the eigenvalues of A2 are x22, x22,…, xn2.
Cyclic Determinants
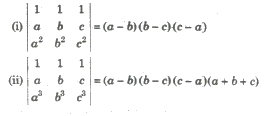
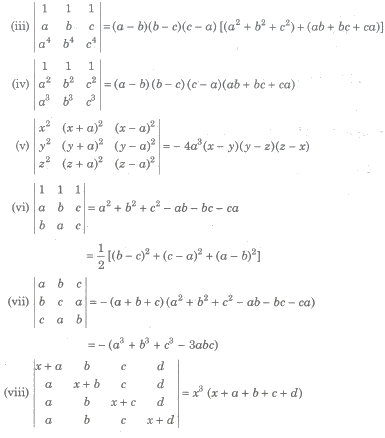
Applications of Determinant in Geometry
Let three points in a plane be A(x1, y1), B(x2, y2) and C(x3, y3), then
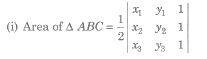
= 1 / 2 [x1 (y2 – y3) + x2 (y3 – y1) + x3 (y1 – y2)]
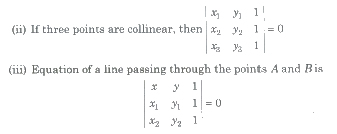
Maximum and Minimum Value of Determinants
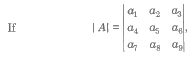
where ais ∈ [α1, α2,…, αn]
Then, |A|max when diagonal elements are
{ min (α1, α2,…, αn)}
and non-diagonal elements are
{ max (α1, α2,…, αn)}
Also, |A|min = – |A|max
Class 12 Key Points, Important Questions & Practice Papers
Hope these notes helped you in your schools exam preparation. Candidates can also check out the Key Points, Important Questions & Practice Papers for various Subjects for Class 12 in both Hindi and English language form the link below.
Class 12 NCERT Solutions
Candidates who are studying in Class 12 can also check Class 12 NCERT Solutions from here. This will help the candidates to know the solutions for all subjects covered in Class 12th. Candidates can click on the subject wise link to get the same. Class 12 Chapter-wise, detailed solutions to the questions of the NCERT textbooks are provided with the objective of helping students compare their answers with the sample answers.
Class 12 Mock Test / Practice
Mock test are the practice test or you can say the blue print of the main exam. Before appearing in the main examination, candidates must try mock test as it helps the students learn from their mistakes. With the help of Class 12 Mock Test / Practice, candidates can also get an idea about the pattern and marking scheme of that examination. For the sake of the candidates we are providing Class 12 Mock Test / Practice links below.
Class 12 Exemplar Questions
Exemplar Questions Class 12 is a very important resource for students preparing for the Examination. Here we have provided Exemplar Problems Solutions along with NCERT Exemplar Problems Class 12. Question from very important topics is covered by Exemplar Questions for Class 12.
Class 12 Maths
Chemistry Notes Physics Notes Biology Notes
To get study material, exam alerts and news, join our Whatsapp Channel.


