Class 12 Physics Atomic Physics – Get here the Notes for Class 12 Physics Atomic Physics. Candidates who are ambitious to qualify the Class 12 with good score can check this article for Notes. This is possible only when you have the best CBSE Class 12 Physics study material and a smart preparation plan. To assist you with that, we are here with notes. Hope these notes will helps you understand the important topics and remember the key points for exam point of view. Below we provided the Notes of Class 12 Physics for topic Atomic Physics.
- Class: 12th
- Subject: Physics
- Topic: Atomic Physics
- Resource: Notes
CBSE Notes Class 12 Physics Atomic Physics
Candidates who are pursuing in Class 12 are advised to revise the notes from this post. With the help of Notes, candidates can plan their Strategy for particular weaker section of the subject and study hard. So, go ahead and check the Important Notes for Class 12 Physics Atomic Physics.
Dalton’s Atomic Theory
All elements are consists of very small invisible particles, called atoms. Atoms of same element are exactly same and atoms of different element are different.
Thomson’s Atomic Model
Every atom is uniformly positive charged sphere of radius of the order of 10-10 m, in which entire mass is uniformly distributed and negative charged electrons are embedded randomly. The atom as a whole is neutral.
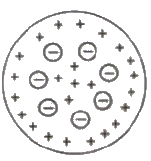
Limitations of Thomson’s Atomic Model
1. It could not explain the origin of spectral series of hydrogen and other atoms.
2. It could not explain large angle scattering of α – particles.
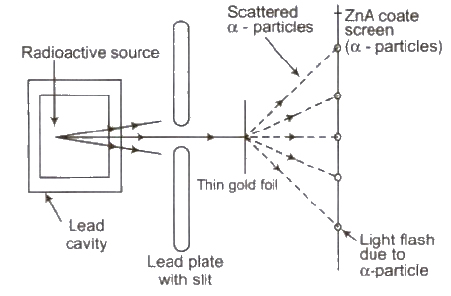
Rutherford’s Atomic Model
On the basis of this experiment, Rutherford made following observations
(i) The entire positive charge and almost entire mass of the atom is concentrated at its centre in a very tiny region of the order of 10-15 m, called nucleus.
(ii) The negatively charged electrons revolve around the nucleus in different orbits.
(iii) The total positive charge 011 nucleus is equal to the total negative charge on electron. Therefore atom as a overall is neutral.
(iv) The centripetal force required by electron for revolution is provided by the electrostatic force of attraction between the electrons and the nucleus.
Distance of Closest Approach
ro = 1 / 4π εo . 2Ze2 / Ek
where, Ek = kinetic energy of the cc-particle.
Impact Parameter
The perpendicular distance of the velocity vector of a-particle from the central line of the nucleus, when the particle is far away from the nucleus is called impact parameter.
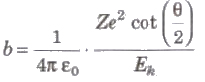
Impact parameter
where, Z = atomic number of the nucleus, Ek = kinetic energy of the c-particle and θ = angle of scattering.
Rutherford’s Scattering Formula
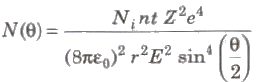
where, N(θ) =number of c-particles, Ni = total number of α-particles reach the screen. n = number of atoms per unit volume in the foil, Z = atoms number, E = kinetic energy of the alpha particles and t = foil thickness

Limitations of Rutherford Atomic Model
(i) About the Stability of Atom According to Maxwell’s electromagnetic wave theory electron should emit energy in the form of electromagnetic wave during its orbital motion. Therefore. radius of orbit of electron will decrease gradually and ultimately it will fall in the nucleus.
(ii) About the Line Spectrum Rutherford atomic model cannot explain atomic line spectrum.
Bohr’s Atomic Model
Electron can revolve in certain non-radiating orbits called stationary or bits for which the angular momentum of electron is an integer multiple of (h / 2π)
mvr = nh / 2π
where n = I, 2. 3,… called principle quantum number.
The radiation of energy occurs only when any electron jumps from one permitted orbit to another permitted orbit.
Energy of emitted photon
hv = E2 – E1
where E1 and E2are energies of electron in orbits.
Radius of orbit of electron is given by
r = n2h2 / 4π2 mK Ze2 ⇒ r ∝ n2 / Z
where, n = principle quantum number, h = Planck’s constant, m = mass of an electron, K = 1 / 4 π ε, Z = atomic number and e = electronic charge.
Velocity of electron in any orbit is given by
v = 2πKZe2 / nh ⇒ v ∝ Z / n
Frequency of electron in any orbit is given by
v = KZe2 / nhr = 4π2Z2e4mK2 / n3 h3
⇒ v prop; Z3 / n3
Kinetic energy of electron in any orbit is given by
Ek = 2π2me4Z2K2 / n2 h2 = 13.6 Z2 / n2 eV
Potential energy of electron in any orbit is given by
Ep = – 4π2me4Z2K2 / n2 h2 = 27.2 Z2 / n2 eV
⇒ Ep = ∝ Z2 / n2
Total energy of electron in any orbit is given by
E = – 2π2me4Z2K2 / n2 h2 = – 13.6 Z2 / n2 eV
⇒ Ep = ∝ Z2 / n2
Wavelength of radiation emitted in the radiation from orbit n2 to n1 is given by

In quantum mechanics, the energies of a system are discrete or quantized. The energy of a particle of mass m is confined to a box of length L can have discrete values of energy given by the relation
En = n2 h2 / 8mL2 ; n < 1, 2, 3,…
Hydrogen Spectrum Series
Each element emits a spectrum of radiation, which is characteristic of the element itself. The spectrum consists of a set of isolated parallel lines and is called the line spectrum.

Hydrogen spectrum contains five series
(i) Lyman Series When electron jumps from n = 2, 3,4, …orbit to n = 1 orbit, then a line of Lyman series is obtained.
This series lies in ultra violet region.
(ii) Balmer Series When electron jumps from n = 3, 4, 5,… orbit to n = 2 orbit, then a line of Balmer series is obtained.
This series lies in visual region.
(iii) Paschen Series When electron jumps from n = 4, 5, 6,… orbit to n = 3 orbit, then a line of Paschen series is obtained.
This series lies in infrared region
(iv) Brackett Series When electron jumps from n = 5,6, 7…. orbit to n = 4 orbit, then a line of Brackett series is obtained.
This series lies in infrared region.
(v) Pfund Series When electron jumps from n = 6,7,8, … orbit to n = 5 orbit, then a line of Pfund series is obtained.
This series lies in infrared region.
Wave Model
It is based on wave mechanics. Quantum numbers are the numbers required to completely specify the state of the electrons.
In the presence of strong magnetic field, the four quantum number are
(i) Principle quantum number (n) can have value 1,2, … ∞
(ii) Orbital angular momentum quantum number l can have value 0,1, 2, … ,(n – 1).
(iii) Magnetic quantum number (me) which can have values – I to I.
(iv) Magnetic spin angular momentum quantum number (ms) which can have only two value + 1 / 2.
Class 12 Key Points, Important Questions & Practice Papers
Hope these notes helped you in your schools exam preparation. Candidates can also check out the Key Points, Important Questions & Practice Papers for various Subjects for Class 12 in both Hindi and English language form the link below.
Class 12 NCERT Solutions
Candidates who are studying in Class 12 can also check Class 12 NCERT Solutions from here. This will help the candidates to know the solutions for all subjects covered in Class 12th. Candidates can click on the subject wise link to get the same. Class 12 Chapter-wise, detailed solutions to the questions of the NCERT textbooks are provided with the objective of helping students compare their answers with the sample answers.
Class 12 Mock Test / Practice
Mock test are the practice test or you can say the blue print of the main exam. Before appearing in the main examination, candidates must try mock test as it helps the students learn from their mistakes. With the help of Class 12 Mock Test / Practice, candidates can also get an idea about the pattern and marking scheme of that examination. For the sake of the candidates we are providing Class 12 Mock Test / Practice links below.
Class 12 Exemplar Questions
Exemplar Questions Class 12 is a very important resource for students preparing for the Examination. Here we have provided Exemplar Problems Solutions along with NCERT Exemplar Problems Class 12. Question from very important topics is covered by Exemplar Questions for Class 12.
To get study material, exam alerts and news, join our Whatsapp Channel.

