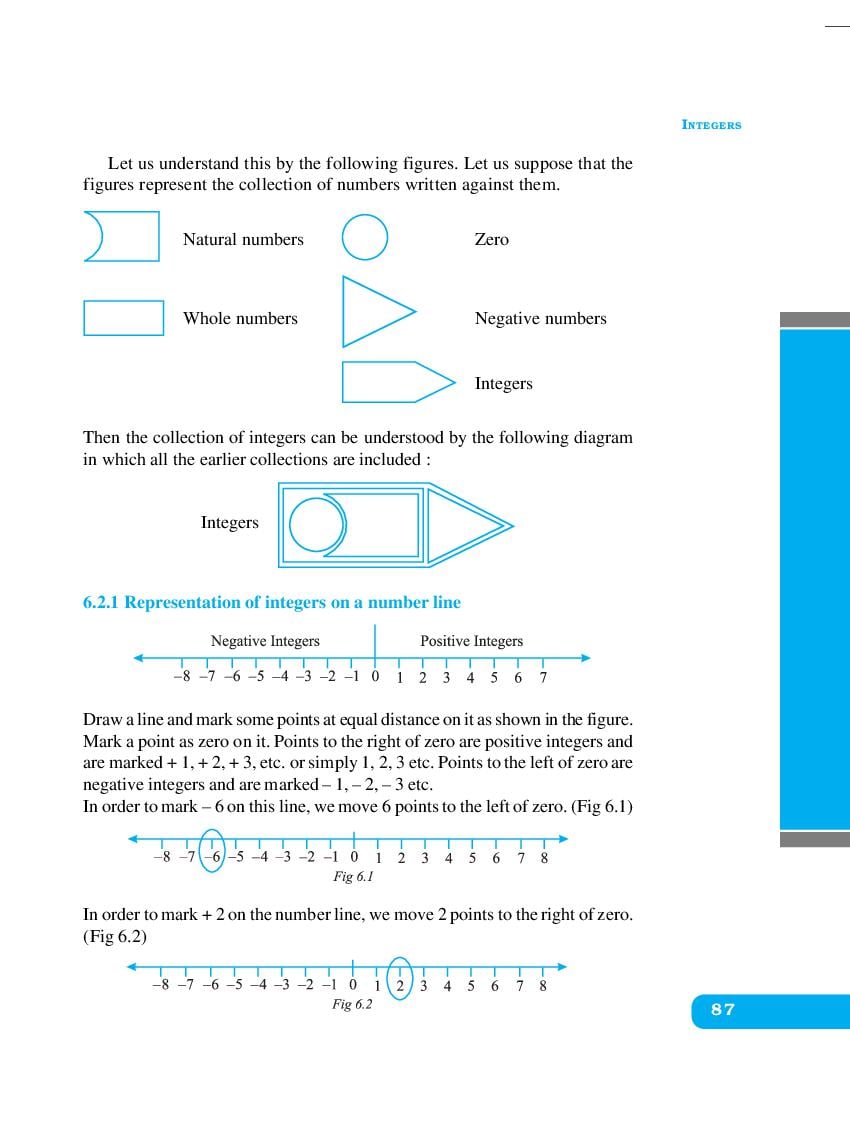
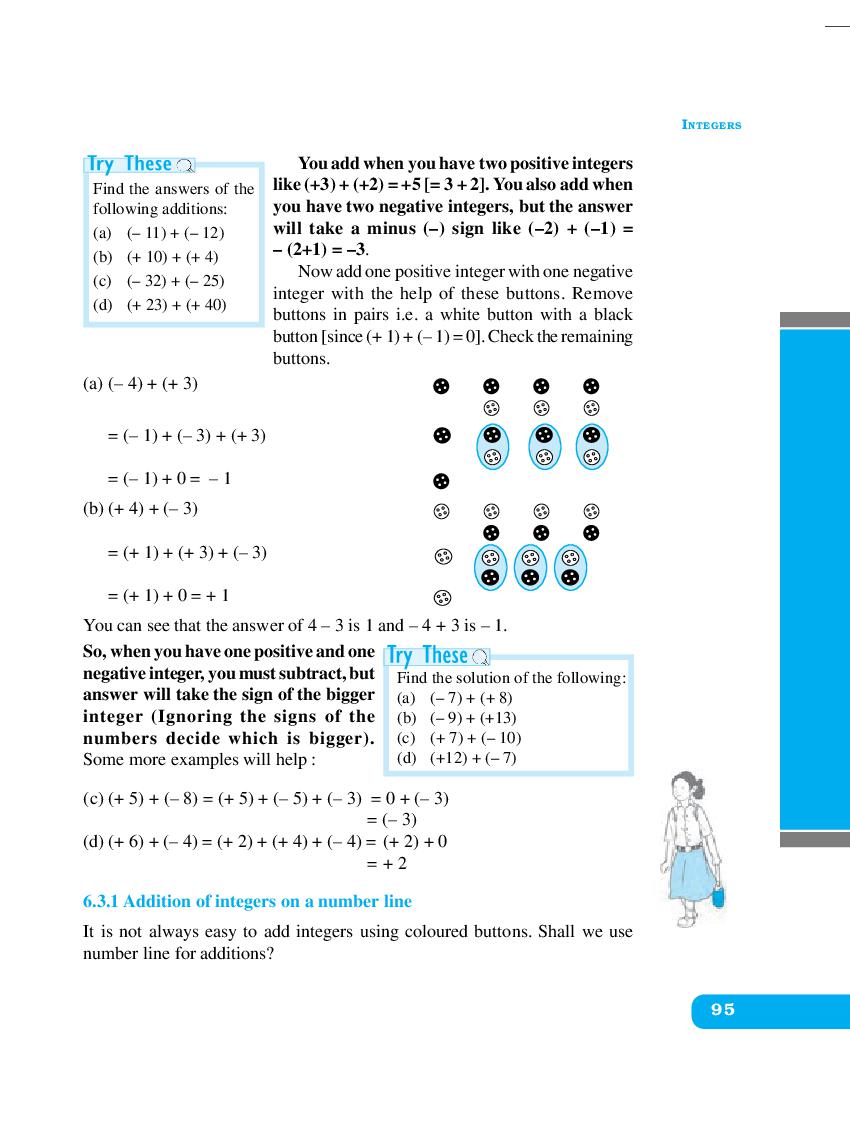
NCERT Book Class 6 Maths Chapter 6 Integers is here. You can read and download Class 6 Maths Chapter 6 PDF from this page of aglasem.com. Integers is one of the many lessons in NCERT Book Class 6 Maths in the new, updated version of 2024. So if you are in 6th standard, and studying Maths textbook (named Mathematics), then you can read Ch 6 here and afterwards use NCERT Solutions to solve questions answers of Integers.
NCERT Book Class 6 Maths Chapter 6 Integers
The complete Chapter 6, which is Integers, from NCERT Books for Class 6 Maths is as follows.
NCERT Book Class 6 Maths Chapter 6 Integers PDF Download Link – Click Here To Download The Complete Chapter PDF
NCERT Book Class 6 Maths Full Book PDF Download Link – Click Here To Download The Complete Book PDF
NCERT Book Class 6 Maths Chapter 6 Integers PDF
The direct link to download class 6 Maths NCERT Book PDF for chapter 6 Integers is given above. However if you want to read the complete lesson on Integers then that is also possible here at aglasem. So here is the complete class 6 Maths Ch 6 Integers.
NCERT Book Class 6 Maths Chapter 6 Integers View DownloadNCERT Book for Class 6 Maths
Besides the chapter on Integers, you can read or download the NCERT Class 6 Maths PDF full book from aglasem. Here is the complete book:
- Chapter 1 Knowning Our Numbers
- Chapter 2 Whole Numbers
- Chapter 3 Playing with Numbers
- Chapter 4 Basic Geometrical Ideas
- Chapter 5 Understanding Elementary Shapes
- Chapter 6 Integers
- Chapter 7 Fractions
- Chapter 8 Decimals
- Chapter 9 Data Handling
- Chapter 10 Mensuration
- Chapter 11 Algebra
- Chapter 12 Ratio and Proportion
NCERT Books for Class 6
Similarly all the subject-wise class 6 books at aglasem.com are as follows.
- NCERT Book Class 6 English
- NCERT Book Class 6 Hindi
- NCERT Book Class 6 Maths
- NCERT Book Class 6 Sanskrit
- NCERT Book Class 6 Science
- NCERT Book Class 6 Social Science
NCERT Books
All class-wise books of National Council of Educational Research and Training are as follows.
- NCERT Books for Class 1
- NCERT Books for Class 2
- NCERT Books for Class 3
- NCERT Books for Class 4
- NCERT Books for Class 5
- NCERT Books for Class 6
- NCERT Books for Class 7
- NCERT Books for Class 8
- NCERT Books for Class 9
- NCERT Books for Class 10
- NCERT Books for Class 11
- NCERT Books for Class 12
Class 6 Maths Chapter 6 Integers NCERT Textbook – An Overview
The highlights of this Integers chapter PDF are as follows.
| Aspects | Details |
|---|---|
| Class | 6 |
| Subject | Maths |
| Book | Mathematics |
| Chapter Number | Ch 6 |
| Chapter Name | Integers |
| Book Portion Here | NCERT Book Class 6 Maths Ch 6 Integers |
| Download Format | |
| Version | NCERT Book (New, Updated) 2024 |
| Complete Book | NCERT Book Class 6 Maths |
| All Class 6 Books | NCERT Books for Class 6 |
| All Textbooks | NCERT Books |
| NCERT Books in Hindi | NCERT Books for Class 6 in Hindi |
| NCERT Solutions | NCERT Solutions for Class 6 |
| More Study Material | Class 6 |
If you have any queries on NCERT Book Class 6 Maths Chapter 6 Integers, then please ask in comments below. And if you found the Class 6 Maths Chapter 6 Integers PDF helpful, then do share with your friends on telegram, facebook, whatsapp, twitter, and other social media! :)
To get study material, exam alerts and news, join our Whatsapp Channel.