Class 12 Maths Matrices – Get here the Notes for Class 12 Maths Matrices. Candidates who are ambitious to qualify the Class 12 with good score can check this article for Notes. Below we have provided the notes of Class 12 Maths for topic Matrices. This is possible only when you have the best CBSE Class 12 Maths Notes, study material, and a smart preparation plan. CBSE 2019 Class 12th Exam is approaching and candidates will have to make the best use of the time available towards the last stage of your CBSE Class 12th Maths Preparation.
- Class: 12th
- Subject: Maths
- Topic: Matrices
- Resource: Notes
CBSE Notes Class 12 Maths Matrices
Candidates who are pursuing in Class 12 are advised to revise the notes from this post. With the help of Notes, candidates can plan their Strategy for particular weaker section of the subject and study hard. So, go ahead and check the Important Notes for Class 12 Maths Matrices
A matrix is a rectangular arrangement of numbers (real or complex) which may be represented as

matrix is enclosed by [ ] or ( ) or | | | |
Compact form the above matrix is represented by [aij]m x n or A = [aij].
- Element of a Matrix The numbers a11, a12 … etc., in the above matrix are known as the element of the matrix, generally represented as aij , which denotes element in ith row and jth column.
- Order of a Matrix In above matrix has m rows and n columns, then A is of order m x n.
Types of Matrices
- Row Matrix A matrix having only one row and any number of columns is called a row matrix.
- Column Matrix A matrix having only one column and any number of rows is called column matrix.
- Rectangular Matrix A matrix of order m x n, such that m ≠ n, is called rectangular matrix.
- Horizontal Matrix A matrix in which the number of rows is less than the number of columns, is called a horizontal matrix.
- Vertical Matrix A matrix in which the number of rows is greater than the number of columns, is called a vertical matrix.
- Null/Zero Matrix A matrix of any order, having all its elements are zero, is called a null/zero matrix. i.e., aij = 0, ∀ i, j
- Square Matrix A matrix of order m x n, such that m = n, is called square matrix.
- Diagonal Matrix A square matrix A = [aij]m x n, is called a diagonal matrix, if all the elements except those in the leading diagonals are zero, i.e., aij = 0 for i ≠ j. It can be represented as
A = diag[a11 a22… ann] - Scalar Matrix A square matrix in which every non-diagonal element is zero and all diagonal elements are equal, is called scalar matrix. i.e., in scalar matrix
aij = 0, for i ≠ j and aij = k, for i = j - Unit/Identity Matrix A square matrix, in which every non-diagonal element is zero and every diagonal element is 1, is called, unit matrix or an identity matrix.
- Upper Triangular Matrix A square matrix A = a[ij]n x n is called a upper triangular matrix, if a[ij], = 0, ∀ i > j.
- Lower Triangular Matrix A square matrix A = a[ij]n x n is called a lower triangular matrix, if a[ij], = 0, ∀ i < j.
- Submatrix A matrix which is obtained from a given matrix by deleting any number of rows or columns or both is called a submatrix of the given matrix.
- Equal Matrices Two matrices A and B are said to be equal, if both having same order and corresponding elements of the matrices are equal.
- Principal Diagonal of a Matrix In a square matrix, the diagonal from the first element of the first row to the last element of the last row is called the principal diagonal of a matrix.
- Singular Matrix A square matrix A is said to be singular matrix, if determinant of A denoted by det (A) or |A| is zero, i.e., |A|= 0, otherwise it is a non-singular matrix.
Algebra of Matrices
1. Addition of Matrices
Let A and B be two matrices each of order m x n. Then, the sum of matrices A + B is defined only if matrices A and B are of same order.
If A = [aij]m x n , A = [aij]m x n
Then, A + B = [aij + bij]m x n
Properties of Addition of Matrices If A, B and C are three matrices of order m x n, then
- Commutative Law A + B = B + A
- Associative Law (A + B) + C = A + (B + C)
- Existence of Additive Identity A zero matrix (0) of order m x n (same as of A), is additive identity, if
A + 0 = A = 0 + A - Existence of Additive Inverse If A is a square matrix, then the matrix (- A) is called additive inverse, if
A + ( – A) = 0 = (- A) + A - Cancellation Law
A + B = A + C ⇒ B = C (left cancellation law)
B + A = C + A ⇒ B = C (right cancellation law)
2. Subtraction of Matrices
Let A and B be two matrices of the same order, then subtraction of matrices, A – B, is defined as
A – B = [aij – bij]n x n,
where A = [aij]m x n, B = [bij]m x n
3. Multiplication of a Matrix by a Scalar
Let A = [aij]m x n be a matrix and k be any scalar. Then, the matrix obtained by multiplying each element of A by k is called the scalar multiple of A by k and is denoted by kA, given as
kA= [kaij]m x n
Properties of Scalar Multiplication If A and B are matrices of order m x n, then
- k(A + B) = kA + kB
- (k1 + k2)A = k1A + k2A
- k1k2A = k1(k2A) = k2(k1A)
- (- k)A = – (kA) = k( – A)
4. Multiplication of Matrices
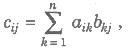
Let A = [aij]m x n and B = [bij]n x p are two matrices such that the number of columns of A is equal to the number of rows of B, then multiplication of A and B is denoted by AB, is given by
where cij is the element of matrix C and C = AB
Properties of Multiplication of Matrices
- Commutative Law Generally AB ≠ BA
- Associative Law (AB)C = A(BC)
- Existence of multiplicative Identity A.I = A = I.A,
I is called multiplicative Identity. - Distributive Law A(B + C) = AB + AC
- Cancellation Law If A is non-singular matrix, then
AB = AC ⇒ B = C (left cancellation law)
BA = CA ⇒B = C (right cancellation law) - AB = 0, does not necessarily imply that A = 0 or B = 0 or both A and B = 0
Important Points to be Remembered
(i) If A and B are square matrices of the same order, say n, then both the product AB and BA are defined and each is a square matrix of order n.
(ii) In the matrix product AB, the matrix A is called premultiplier (prefactor) and B is called postmultiplier (postfactor).
(iii) The rule of multiplication of matrices is row column wise (or → ↓ wise) the first row of AB is obtained by multiplying the first row of A with first, second, third,… columns of B respectively; similarly second row of A with first, second, third, … columns of B, respectively and so on.
Positive Integral Powers of a Square Matrix
Let A be a square matrix. Then, we can define
- An + 1 = An. A, where n ∈ N.
- Am. An = Am + n
- (Am)n = Amn, ∀ m, n ∈ N
Matrix Polynomial
Let f(x)= a0xn + a1xn – 1 -1 + a2xn – 2 + … + an. Then
f(A)= a0An + a1An – 2 + … + anIn
is called the matrix polynomial.
Transpose of a Matrix
Let A = [aij]m x n, be a matrix of order m x n. Then, the n x m matrix obtained by interchanging the rows and columns of A is called the transpose of A and is denoted by A’ or AT.
A’ = AT = [aij]n x m
Properties of Transpose
- (A’)’ = A
- (A + B)’ = A’ + B’
- (AB)’ = B’A’
- (KA)’ = kA’
- (AN)’ = (A’)N
- (ABC)’ = C’ B’ A’
Symmetric and Skew-Symmetric Matrices
- A square matrix A = [aij]n x n, is said to be symmetric, if A’ = A.
i.e., aij = aji , ∀i and j. - A square matrix A is said to be skew-symmetric matrices, if i.e., aij = — aji, di and j
Properties of Symmetric and Skew-Symmetric Matrices
- Elements of principal diagonals of a skew-symmetric matrix are all zero. i.e., aii = — aii 2ii = 0 or aii = 0, for all values of i.
- If A is a square matrix, then
(a) A + A’ is symmetric.
(b) A — A’ is skew-symmetric matrix. - If A and B are two symmetric (or skew-symmetric) matrices of same order, then A + B is also symmetric (or skew-symmetric).
- If A is symmetric (or skew-symmetric), then kA (k is a scalar) is also symmetric for skew-symmetric matrix.
- If A and B are symmetric matrices of the same order, then the product AB is symmetric, iff BA = AB.
- Every square matrix can be expressed uniquely as the sum of a symmetric and a skew-symmetric matrix.
- The matrix B’ AB is symmetric or skew-symmetric according as A is symmetric or skew-symmetric matrix.
- All positive integral powers of a symmetric matrix are symmetric.
- All positive odd integral powers of a skew-symmetric matrix are skew-symmetric and positive even integral powers of a skew-symmetric are symmetric matrix.
- If A and B are symmetric matrices of the same order, then
(a) AB – BA is a skew-symmetric and
(b) AB + BA is symmetric. - For a square matrix A, AA’ and A’ A are symmetric matrix.
Trace of a Matrix
The sum of the diagonal elements of a square matrix A is called the trace of A, denoted by trace (A) or tr (A).
Properties of Trace of a Matrix
- Trace (A ± B)= Trace (A) ± Trace (B)
- Trace (kA)= k Trace (A)
- Trace (A’ ) = Trace (A)
- Trace (In)= n
- Trace (0) = 0
- Trace (AB) ≠ Trace (A) x Trace (B)
- Trace (AA’) ≥ 0
Conjugate of a Matrix
The matrix obtained from a matrix A containing complex number as its elements, on replacing its elements by the corresponding conjugate complex number is called conjugate of A and is denoted by A.
Properties of Conjugate of a Matrix
If A is a matrix of order m x n, then

Transpose Conjugate of a Matrix
The transpose of the conjugate of a matrix A is called transpose conjugate of A and is denoted by A0 or A*.
i.e., (A’) = A’ = A0 or A*
Properties of Transpose Conjugate of a Matrix
(i) (A*)* = A
(ii) (A + B)* = A* + B*
(iii) (kA)* = kA*
(iv) (AB)* = B*A*
(V) (An)* = (A*)n
Some Special Types of Matrices
1. Orthogonal Matrix
A square matrix of order n is said to be orthogonal, if AA’ = In = A’A Properties of Orthogonal Matrix
(i) If A is orthogonal matrix, then A’ is also orthogonal matrix.
(ii) For any two orthogonal matrices A and B, AB and BA is also an orthogonal matrix.
(iii) If A is an orthogonal matrix, A-1 is also orthogonal matrix.
2. ldempotent Matrix
A square matrix A is said to be idempotent, if A2 = A.
Properties of Idempotent Matrix
(i) If A and B are two idempotent matrices, then
- AB is idempotent, if AB = BA.
- A + B is an idempotent matrix, iff
AB = BA = 0 - AB = A and BA = B, then A2 = A, B2 = B
(ii)
- If A is an idempotent matrix and A + B = I, then B is an idempotent and AB = BA= 0.
- Diagonal (1, 1, 1, …,1) is an idempotent matrix.
- If I1, I2 and I3 are direction cosines, then
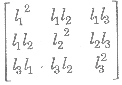
is an idempotent as |Δ|2 = 1.
A square matrix A is said to be involutory, if A2 = I
4. Nilpotent Matrix
A square matrix A is said to be nilpotent matrix, if there exists a positive integer m such that A2 = 0. If m is the least positive integer such that Am = 0, then m is called the index of the nilpotent matrix A.
5. Unitary Matrix
A square matrix A is said to be unitary, if A’A = I
Hermitian Matrix
A square matrix A is said to be hermitian matrix, if A = A* or
= aij, for aji only.
Properties of Hermitian Matrix
- If A is hermitian matrix, then kA is also hermitian matrix for any non-zero real number k.
- If A and B are hermitian matrices of same order, then λ1A + λB, also hermitian for any non-zero real number λ1, and λ.
- If A is any square matrix, then AA* and A* A are also hermitian.
- If A and B are hermitian, then AB is also hermitian, iff AB = BA
- If A is a hermitian matrix, then A is also hermitian.
- If A and B are hermitian matrix of same order, then AB + BA is also hermitian.
- If A is a square matrix, then A + A* is also hermitian,
- Any square matrix can be uniquely expressed as A + iB, where A and B are hermitian matrices.
Skew-Hermitian Matrix
A square matrix A is said to be skew-hermitian if A* = – A or aji for every i and j.
Properties of Skew-Hermitian Matrix
- If A is skew-hermitian matrix, then kA is skew-hermitian matrix, where k is any non-zero real number.
- If A and B are skew-hermitian matrix of same order, then λ1A + λ2B is also skew-hermitian for any real number λ1 and λ2.
- If A and B are hermitian matrices of same order, then AB — BA is skew-hermitian.
- If A is any square matrix, then A — A* is a skew-hermitian matrix.
- Every square matrix can be uniquely expressed as the sum of a hermitian and a skew-hermitian matrices.
- If A is a skew-hermitian matrix, then A is a hermitian matrix.
- If A is a skew-hermitian matrix, then A is also skew-hermitian matrix.
Adjoint of a Square Matrix
Let A[aij]m x n be a square matrix of order n and let Cij be the cofactor of aij in the determinant |A| , then the adjoint of A, denoted by adj (A), is defined as the transpose of the matrix, formed by the cofactors of the matrix.
Properties of Adjoint of a Square Matrix
If A and B are square matrices of order n, then
- A (adj A) = (adj A) A = |A|I
- adj (A’) = (adj A)’
- adj (AB) = (adj B) (adj A)
- adj (kA) = kn – 1(adj A), k ∈ R
- adj (Am) = (adj A)m
- adj (adj A) = |A|n – 2 A, A is a non-singular matrix.
- |adj A| =|A|n – 1 ,A is a non-singular matrix.
- |adj (adj A)| =|A|(n – 1)2 A is a non-singular matrix.
- Adjoint of a diagonal matrix is a diagonal matrix.
Inverse of a Square Matrix

Let A be a square matrix of order n, then a square matrix B, such that AB = BA = I, is called inverse of A, denoted by A-1.
i.e.,
or AA-1 = A-1A = 1
Properties of Inverse of a Square Matrix
- Square matrix A is invertible if and only if |A| ≠ 0
- (A-1)-1 = A
- (A’)-1 = (A-1)’
- (AB)-1 = B-1A-1
In general (A1A1A1 … An)-1 = An-1An – 1-1 … A3-1A2-1A1-1 - If a non-singular square matrix A is symmetric, then A-1 is also symmetric.
- |A-1| = |A|-1
- AA-1 = A-1A = I
- (Ak)-1 = (A-1)Ak k ∈ N
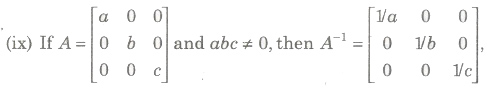
Elementary Transformation
Any one of the following operations on a matrix is called an elementary transformation.
- Interchanging any two rows (or columns), denoted by Ri←→Rj or Ci←→Cj
- Multiplication of the element of any row (or column) by a non-zero quantity and denoted by
Ri → kRi or Ci → kCj - Addition of constant multiple of the elements of any row to the corresponding element of any other row, denoted by
Ri → Ri + kRj or Ci → Ci + kCj
Equivalent Matrix
- Two matrices A and B are said to be equivalent, if one can be obtained from the other by a sequence of elementary transformation.
- The symbol≈ is used for equivalence.
Rank of a Matrix
A positive integer r is said to be the rank of a non-zero matrix A, if
- there exists at least one minor in A of order r which is not zero.
- every minor in A of order greater than r is zero, rank of a matrix A is denoted by ρ(A) = r.
Properties of Rank of a Matrix
- The rank of a null matrix is zero ie, ρ(0) = 0
- If In is an identity matrix of order n, then ρ(In) = n.
- (a) If a matrix A does’t possess any minor of order r, then ρ(A) ≥ r.
(b) If at least one minor of order r of the matrix is not equal to zero, then ρ(A) ≤ r. - If every (r + 1)th order minor of A is zero, then any higher order – minor will also be zero.
- If A is of order n, then for a non-singular matrix A, ρ(A) = n
- ρ(A’)= ρ(A)
- ρ(A*) = ρ(A)
- ρ(A + B) &LE; ρ(A) + ρ(B)
- If A and B are two matrices such that the product AB is defined, then rank (AB) cannot exceed the rank of the either matrix.
- If A and B are square matrix of same order and ρ(A) = ρ(B) = n, then p(AB)= n
- Every skew-symmetric matrix,of odd order has rank less than its order.
- Elementary operations do not change the rank of a matrix.
Echelon Form of a Matrix
A non-zero matrix A is said to be in Echelon form, if A satisfies the following conditions
- All the non-zero rows of A, if any precede the zero rows.
- The number of zeros preceding the first non-zero element in a row is less than the number of such zeros in the successive row.
- The first non-zero element in a row is unity.
- The number of non-zero rows of a matrix given in the Echelon form is its rank.
Homogeneous and Non-Homogeneous System of Linear Equations
A system of equations AX = B, is called a homogeneous system if B = 0 and if B ≠ 0, then it is called a non-homogeneous system of equations.
Solution of System of Linear Equations
The values of the variables satisfying all the linear equations in the system, is called solution of system of linear equations.
1 . Solution of System of Equations by Matrix Method
(i) Non-Homogeneous System of Equations Let AX = B be a system of n linear equations in n variables.
- If |A| ≠ 0, then the system of equations is consistent and has a unique solution given by X = A-1B.
- If |A| = 0 and (adj A)B = 0, then the system of equations is consistent and has infinitely many solutions.
- If |A| = 0 and (adj A) B ≠ 0, then the system of equations is inconsistent i.e., having no solution
(ii) Homogeneous System of Equations Let AX = 0 is a system of n linear equations in n variables.
- If I |A| ≠ 0, then it has only solution X = 0, is called the trivial solution.
- If I |A| = 0, then the system has infinitely many solutions, called non-trivial solution.
2. Solution of System of Equations by Rank Method
(i) Non-Homogeneous System of Equations Let AX = B, be a system of n linear equations in n variables, then
- Step I Write the augmented matrix [A:B]
- Step II Reduce the augmented matrix to Echelon form using elementary row-transformation.
- Step III Determine the rank of coefficient matrix A and augmented matrix [A:B] by counting the number of non-zero rows in A and [A:B].
Important Results
- If ρ(A) ≠ ρ(AB), then the system of equations is inconsistent.
- If ρ(A) =ρ(AB) = the number of unknowns, then the system of equations is consistent and has a unique solution.
- If ρ(A) = ρ(AB) < the number of unknowns, then the system of equations is consistent and has infinitely many solutions.
(ii) Homogeneous System of Equations
- If AX = 0, be a homogeneous system of linear equations then, If ρ(A) = number of unknown, then AX = 0, have a non-trivial solution, i.e., X = 0.
- If ρ(A) < number of unknowns, then AX = 0, have a non-trivial solution, with infinitely many solutions.
Class 12 Key Points, Important Questions & Practice Papers
Hope these notes helped you in your schools exam preparation. Candidates can also check out the Key Points, Important Questions & Practice Papers for various Subjects for Class 12 in both Hindi and English language form the link below.
Class 12 NCERT Solutions
Candidates who are studying in Class 12 can also check Class 12 NCERT Solutions from here. This will help the candidates to know the solutions for all subjects covered in Class 12th. Candidates can click on the subject wise link to get the same. Class 12 Chapter-wise, detailed solutions to the questions of the NCERT textbooks are provided with the objective of helping students compare their answers with the sample answers.
Class 12 Mock Test / Practice
Mock test are the practice test or you can say the blue print of the main exam. Before appearing in the main examination, candidates must try mock test as it helps the students learn from their mistakes. With the help of Class 12 Mock Test / Practice, candidates can also get an idea about the pattern and marking scheme of that examination. For the sake of the candidates we are providing Class 12 Mock Test / Practice links below.
Class 12 Exemplar Questions
Exemplar Questions Class 12 is a very important resource for students preparing for the Examination. Here we have provided Exemplar Problems Solutions along with NCERT Exemplar Problems Class 12. Question from very important topics is covered by Exemplar Questions for Class 12.
Class 12 Maths
Chemistry Notes Physics Notes Biology Notes
To get study material, exam alerts and news, join our Whatsapp Channel.




