CBSE Class 11 Maths Sets, Relations and Binary Operations – Get here the Notes for Class 11 Sets, Relations and Binary Operations. Candidates who are ambitious to qualify the Class 11 with good score can check this article for Notes. This is possible only when you have the best CBSE Class 11 Maths study material and a smart preparation plan. To assist you with that, we are here with notes. Hope these notes will helps you understand the important topics and remember the key points for exam point of view. Below we provided the Notes of CBSE Class 11 Maths for topic Sets, Relations and Binary Operations.
- Class: 11th
- Subject: Maths
- Topic: Sets, Relations and Binary Operations
- Resource: Notes
CBSE Notes Class 11 Maths Sets, Relations and Binary Operations
Candidates who are pursuing in CBSE Class 11 Maths are advised to revise the notes from this post. With the help of Notes, candidates can plan their Strategy for particular weaker section of the subject and study hard. So, go ahead and check the Important Notes for Class 11 Maths Sets, Relations and Binary Operations from this article.
Set
Set is a collection of well defined objects which are distinct from each other. Sets are usually denoted by capital letters A, B,C,… and elements are usually denoted by small letters a, b,c,… .
If ‘a’ is an element of a set A, then we write a ∈ A and say ‘a’ belongs to A or ‘a’ is in A or ‘a’ is a member of A. If ‘a’ does not belongs to A, we write a ∉ A.
Standard Notations
- N : A set of natural numbers.
- W : A set of whole numbers.
- Z : A set of integers.
- Z+/Z– : A set of all positive/negative integers.
- Q : A set of all rational numbers.
- Q+/Q– : A set of all positive/ negative rational numbers.
- R : A set of real numbers.
- R+/R–: A set of all positive/negative real numbers.
- C : A set of all complex numbers.
Methods for Describing a Set
(i) Roster/Listing Method/Tabular Form In this method, a set is described by listing element, separated by commas, within braces.
e.g., A = {a, e, i, o, u}
(ii) Set Builder/Rule Method In this method, we write down a property or rule which gives us all the elements of the set by that rule.
e.g.,A = {x : x is a vowel of English alphabets}
Types of Sets
- Finite Set A set containing finite number of elements or no element.
- Cardinal Number of a Finite Set The number of elements in a given finite set is called cardinal number of finite set, denoted by n (A).
- Infinite Set A set containing infinite number of elements.
- Empty/Null/Void Set A set containing no element, it is denoted by (φ) or { }.
- Singleton Set A set containing a single element.
- Equal Sets Two sets A and B are said to be equal, if every element of A is a member of B and every element of B is a member of A and we write A = B.
- Equivalent Sets Two sets are said to be equivalent, if they have same number of elements.
If n(A) = n(B), then A and B are equivalent sets. But converse is not true. - Subset and Superset Let A and B be two sets. If every element of A is an element of B, then A is called subset of B and B is called superset of A. Written as
A ⊆ B or B ⊇ A - Proper Subset If A is a subset of B and A ≠ B, then A is called proper subset of B and we write A ⊂ B.
- Universal Set (U) A set consisting of all possible elements which occurs under consideration is called a universal set.
- Comparable Sets Two sets A and Bare comparable, if A ⊆ B or B ⊆ A.
- Non-Comparable Sets For two sets A and B, if neither A ⊆ B nor B ⊆ A, then A and B are called non-comparable sets.
- Power Set (P) The set formed by all the subsets of a given set A, is called power set of A, denoted by P(A).
- Disjoint Sets Two sets A and B are called disjoint, if, A ∩ B = (φ).
Venn Diagram
In a Venn diagram, the universal set is represented by a rectangular region and a set is represented by circle or a closed geometrical figure inside the universal set.
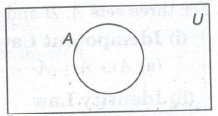
Operations on Sets
1. Union of Sets
The union of two sets A and B, denoted by A ∪ B is the set of all those elements, each one of which is either in A or in B or both in A and B.
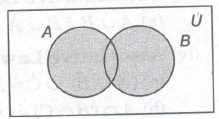
2. Intersection of Sets
The intersection of two sets A and B, denoted by A ∩ B, is the set of all those elements which are common to both A and B.
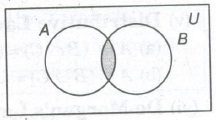
If A1, A2,… , An is a finite family of sets, then their intersection is denoted by
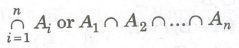
3. Complement of a Set
If A is a set with U as universal set, then complement of a set, denoted by A’ or Ac is the set U – A .
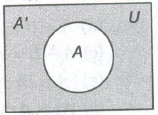
4. Difference of Sets
For two sets A and B, the difference A – B is the set of all those elements of A which do not belong to B.
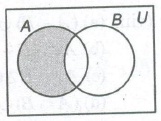
5. Symmetric Difference
For two sets A and B, symmetric difference is the set (A – B) ∪ (B – A) denoted by A Δ B.
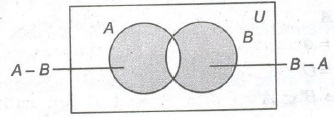
Laws of Algebra of Sets
For three sets A, B and C
(i) Commutative Laws
A ∩ B = B ∩ A
A ∪ B = B ∪ A
(ii) Associative Laws
(A ∩ B) ∩ C = A ∩ (B ∩ C)
(A ∪ B) ∪ C = A ∪ (B ∪ C)
(iii) Distributive Laws
A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C)
A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C)
(iv) Idempotent Laws
A ∩ A = A
A ∪ A = A
(v) Identity Laws
A ∪ Φ = A
A ∩ U = A
(vi) De Morgan’s Laws
(a) (A ∩ B) ′ = A ′ ∪ B ′
(b) (A ∪ B) ′ = A ′ ∩ B ′
(c) A – (B ∩ C) = (A – B) ∩ (A- C)
(d) A – (B ∪ C) = (A – B) ∪ ( A – C)
(vii) (a) A – B = A ∩ B’
(b) B – A = B ∩ A’
(c) A – B = A ⇔A ∩ B= (Φ)
(d) (A – B) ∪ B= A ∪ B
(e) (A – B) ∩ B = (Φ)
(f) A ∩ B ⊆ A and A ∩ B ⊆ B
(g) A ∪ (A ∩ B)= A
(h) A ∩ (A ∪ B)= A
(viii) (a) (A – B) ∪ (B – A) = (A ∪ B) – (A ∩ B)
(b) A ∩ (B – C) = (A ∩ B) – (A ∩ C)
(c) A ∩ (B Δ C) = (A ∩ B) A (A ∩ C)
(d) (A ∩ B) ∪ (A – B) = A
(e) A ∪ (B – A) = (A ∪ B)
(ix) (a) U’ = (Φ)
(b) Φ’ = U
(c) (A’ )’ = A
(d) A ∩ A’ = (Φ)
(e) A ∪ A’ = U
(f) A ⊆ B ⇔ B’ ⊆ A’
Important Points to be Remembered
- Every set is a subset of itself i.e., A ⊆ A, for any set A.
- Empty set Φ is a subset of every set i.e., Φ ⊂ A, for any set A.
- For any set A and its universal set U, A ⊆ U
- If A = Φ, then power set has only one element i.e., n(P(A)) = 1
- Power set of any set is always a non-empty set.
Suppose A = {1, 2}, thenP(A) = {{1}, {2}, {1, 2}, Φ}.(a) A ∉ P(A)
(b) {A} ∈ P(A) - (vii) If a set A has n elements, then P(A) or subset of A has 2n elements.
- (viii) Equal sets are always equivalent but equivalent sets may not be equal.
The set {Φ} is not a null set. It is a set containing one element Φ.
Results on Number of Elements in Sets
- n (A ∪ B) = n(A) + (B)- n(A ∩ B)
- n(A ∪ B) = n(A)+ n(B), if A and B are disjoint.
- n(A – B) = n(A) – n(A ∩ B)
- n(A Δ B) = n(A) + n(B)- 2n(A ∩ B)
- n(A ∪ B ∪ C)= n(A)+ n(B)+ n(C)- n(A ∩ B) – n(B ∩ C)- n(A ∩ C)+ n(A ∩ B ∩ C)
- n (number of elements in exactly two of the sets A, B, C) = n(A ∩ B) + n(B ∩ C) + n (C ∩ A)- 3n(A ∩ B ∩ C)
- n (number of elements in exactly one of the sets A, B, C) = n(A) + n(B) + n(C) – 2n(A ∩ B) – 2n(B ∩ C) – 2n(A ∩ C) + 3n(A ∩ B ∩ C)
- n(A’ ∪ B’)= n(A ∩ B)’ = n(U) – n(A ∩ B)
- n(A’ ∩ B’ ) = n(A ∪ B)’ = n(U) – n(A ∪ B)
- n(B – A) = n(B)- n(A ∩ B)
Ordered Pair
An ordered pair consists of two objects or elements in a given fixed order.
Equality of Ordered Pairs Two ordered pairs (a1, b1) and (a2, b2) are equal iff a1 = a2 and b1 = b2.
Cartesian Product of Sets
For two sets A and B (non-empty sets), the set of all ordered pairs (a, b) such that a ∈ A and b ∈ B is called Cartesian product of the sets A and’ B, denoted by A x B.
A x B={(a,b):a ∈ A and b ∈ B}
If there are three sets A, B, C and a ∈ A, be B and c ∈ C, then we form, an ordered triplet (a, b, c). The set of all ordered triplets (a, b, c) is called the cartesian product of these sets A, B and C.
i.e., A x B x C = {(a,b,c):a ∈ A,b ∈ B,c ∈ C}
Properties of Cartesian Product
For three sets A, B and C
- n (A x B)= n(A) n(B)
- A x B = Φ, if either A or B is an empty set.
- A x (B ∪ C)= (A x B) ∪ (A x C)
- A x (B ∩ C) = (A x B) ∩ (A x C)
- A x (B — C)= (A x B) — (A x C)
- (A x B) ∩ (C x D)= (A ∩ C) x (B ∩ D)
- If A ⊆ B and C ⊆ D, then (A x C) ⊂ (B x D)
- If A ⊆ B, then A x A ⊆ (A x B) ∩ (B x A)
- A x B = B x A ⇔ A = B
- If either A or B is an infinite set, then A x B is an infinite set.
- A x (B’ ∪ C’ )’ = (A x B) ∩ (A x C)
- A x (B’ ∩ C’ )’ = (A x B) ∪ (A x C)
- If A and B be any two non-empty sets having n elements in common, then A x B and B x A have n2 elements in common.
- If ≠ B, then A x B ≠ B x A
- If A = B, then A x B= B x A
- If A ⊆ B, then A x C = B x C for any set C.
Relation
If A and B are two non-empty sets, then a relation R from A to B is a subset of A x B.
If R ⊆ A x B and (a, b) ∈ R, then we say that a is related to b by the relation R, written as aRb.
Domain and Range of a Relation
Let R be a relation from a set A to set B. Then, set of all first components or coordinates of the ordered pairs belonging to R is called : the domain of R, while the set of all second components or coordinates = of the ordered pairs belonging to R is called the range of R.
Thus, domain of R = {a : (a , b) ∈ R} and range of R = {b : (a, b) ∈ R}
Types of Relations
(i) Void Relation As Φ ⊂ A x A, for any set A, so Φ is a relation on A, called the empty or void relation.
(ii) Universal Relation Since, A x A ⊆ A x A, so A x A is a relation on A, called the universal relation.
(iii) Identity Relation The relation IA = {(a, a) : a ∈ A} is called the identity relation on A.
(iv) Reflexive Relation A relation R is said to be reflexive relation, if every element of A is related to itself.
Thus, (a, a) ∈ R, ∀ a ∈ A = R is reflexive.
(v) Symmetric Relation A relation R is said to be symmetric relation, iff
(a, b) ∈ R (b, a) ∈ R,∀ a, b ∈ A
i.e., a R b ⇒ b R a,∀ a, b ∈ A
⇒ R is symmetric.
(vi) Anti-Symmetric Relation A relation R is said to be anti-symmetric relation, iff
(a, b) ∈ R and (b, a) ∈ R ⇒ a = b,∀ a, b ∈ A
(vii) Transitive Relation A relation R is said to be transitive relation, iff (a, b) ∈ R and (b, c) ∈ R
⇒ (a, c) ∈ R, ∀ a, b, c ∈ A
(viii) Equivalence Relation A relation R is said to be an equivalence relation, if it is simultaneously reflexive, symmetric and transitive on A.
(ix) Partial Order Relation A relation R is said to be a partial order relation, if it is simultaneously reflexive, symmetric and anti-symmetric on A.
(x) Total Order Relation A relation R on a set A is said to be a total order relation on A, if R is a partial order relation on A.
Inverse Relation
If A and B are two non-empty sets and R be a relation from A to B, such that R = {(a, b) : a ∈ A, b ∈ B}, then the inverse of R, denoted by R-1 , i a relation from B to A and is defined by
R-1 = {(b, a) : (a, b) ∈ R}
Equivalence Classes of an Equivalence Relation
Let R be equivalence relation in A (≠ Φ). Let a ∈ A.
Then, the equivalence class of a denoted by [a] or {a} is defined as the set of all those points of A which are related to a under the relation R.
Composition of Relation
Let R and S be two relations from sets A to B and B to C respectively, then we can define relation SoR from A to C such that (a, c) ∈ So R ⇔ ∃ b ∈ B such that (a, b) ∈ R and (b, c) ∈ S.
This relation SoR is called the composition of R and S.
(i) RoS ≠ SoR
(ii) (SoR)-1 = R-1oS-1
known as reversal rule.
Congruence Modulo m
Let m be an arbitrary but fixed integer. Two integers a and b are said to be congruence modulo m, if a – b is divisible by m and we write a ≡ b (mod m).
i.e., a ≡ b (mod m) ⇔ a – b is divisible by m.
Important Results on Relation
- If R and S are two equivalence relations on a set A, then R ∩ S is also on ‘equivalence relation on A.
- The union of two equivalence relations on a set is not necessarily an equivalence relation on the set.
- If R is an equivalence relation on a set A, then R-1 is also an equivalence relation on A.
- If a set A has n elements, then number of reflexive relations from A to A is 2n2 – 2
- Let A and B be two non-empty finite sets consisting of m and n elements, respectively. Then, A x B consists of mn ordered pairs. So, total number of relations from A to B is 2nm.
Binary Operations
Closure Property
An operation * on a non-empty set S is said to satisfy the closure ‘ property, if
a ∈ S, b ∈ S ⇒ a * b ∈ S, ∀ a, b ∈ S
Also, in this case we say that S is closed for *.
An operation * on a non-empty set S, satisfying the closure property is known as a binary operation.
or
Let S be a non-empty set. A function f from S x S to S is called a binary operation on S i.e., f : S x S → S is a binary operation on set S.
Properties
- Generally binary operations are represented by the symbols * , +, … etc., instead of letters figure etc.
- Addition is a binary operation on each one of the sets N, Z, Q, R and C of natural numbers, integers, rationals, real and complex numbers, respectively. While addition on the set S of all irrationals is not a binary operation.
- Multiplication is a binary operation on each one of the sets N, Z, Q, R and C of natural numbers, integers, rationals, real and complex numbers, respectively. While multiplication on the set S of all irrationals is not a binary operation.
- Subtraction is a binary operation on each one of the sets Z, Q, R and C of integers, rationals, real and complex numbers, respectively. While subtraction on the set of natural numbers is not a binary operation.
- Let S be a non-empty set and P(S) be its power set. Then, the union and intersection on P(S) is a binary operation.
- Division is not a binary operation on any of the sets N, Z, Q, R and C. However, it is not a binary operation on the sets of all non-zero rational (real or complex) numbers.
- Exponential operation (a, b) → ab is a binary operation on set N of natural numbers while it is not a binary operation on set Z of integers.
Types of Binary Operations
(i) Associative Law A binary operation * on a non-empty set S is said to be associative, if (a * b) * c = a * (b * c), ∀ a, b, c ∈ S.
Let R be the set of real numbers, then addition and multiplication on R satisfies the associative law.
(ii) Commutative Law A binary operation * on a non-empty set S is said to be commutative, if
a * b = b * a, ∀ a, b ∈ S.
Addition and multiplication are commutative binary operations on Z but subtraction not a commutative binary operation, since
2 — 3 ≠ 3— 2 .
Union and intersection are commutative binary operations on the power P(S) of all subsets of set S. But difference of sets is not a commutative binary operation on P(S).
(iii) Distributive Law Let * and o be two binary operations on a non-empty sets. We say that * is distributed over o., if
a * (b o c)= (a * b) o (a * c), ∀ a, b, c ∈ S also called (left distribution) and (b o c) * a = (b * a) o (c * a), ∀ a, b, c ∈ S also called (right distribution).
Let R be the set of all real numbers, then multiplication distributes addition on R.
Since, a.(b + c) = a.b + a.c,∀ a, b, c ∈ R.
(iv) Identity Element Let * be a binary operation on a non-empty set S. An element e a S, if it exist such that
a * e = e * a = a, ∀ a ∈ S.
is called an identity elements of S, with respect to *.
For addition on R, zero is the identity elements in R.
Since, a + 0 = 0 + a = a, ∀ a ∈ R
For multiplication on R, 1 is the identity element in R.
Since, a x 1 =1 x a = a,∀ a ∈ R
Let P (S) be the power set of a non-empty set S. Then, Φ is the identity element for union on P (S) as
A ∪ Φ =Φ ∪ A = A, ∀ A ∈ P(S)
Also, S is the identity element for intersection on P(S).
Since, A ∩ S=A ∩ S=A, ∀ A ∈ P(S).
For addition on N the identity element does not exist. But for multiplication on N the idenitity element is 1.
(v) Inverse of an Element Let * be a binary operation on a non-empty set ‘S’ and let ‘e’ be the identity element.
Let a ∈ S. we say that a-1 is invertible, if there exists an element b ∈ S such that a * b = b * a = e
Also, in this case, b is called the inverse of a and we write, a-1 = b
Addition on N has no identity element and accordingly N has no invertible element.
Multiplication on N has 1 as the identity element and no element other than 1 is invertible.
Let S be a finite set containing n elements. Then, the total number of binary operations on S in nn2
Let S be a finite set containing n elements. Then, the total number of commutative binary operation on S is n [n(n+1)/2].
Class 11 Key Points, Important Questions & Practice Papers
Hope these notes helped you in your schools exam preparation. Candidates can also check out the Key Points, Important Questions & Practice Papers for various Subjects for Class 11 in both Hindi and English language form the link below.
Class 11 NCERT Solutions
Candidates who are studying in Class 11 can also check Class 11 NCERT Solutions from here. This will help the candidates to know the solutions for all subjects covered in Class 11th. Candidates can click on the subject wise link to get the same. Class 11 Chapter-wise, detailed solutions to the questions of the NCERT textbooks are provided with the objective of helping students compare their answers with the sample answers.
Class 11 Mock Test / Practice
Mock test are the practice test or you can say the blue print of the main exam. Before appearing in the main examination, candidates must try mock test as it helps the students learn from their mistakes. With the help of Class 11 Mock Test / Practice, candidates can also get an idea about the pattern and marking scheme of that examination. For the sake of the candidates we are providing Class 11 Mock Test / Practice links below.
Class 11 Exemplar Questions
Exemplar Questions Class 11 is a very important resource for students preparing for the Examination. Here we have provided Exemplar Problems Solutions along with NCERT Exemplar Problems Class 11. Question from very important topics is covered by Exemplar Questions for Class 11.
CBSE Notes for Class 11 Maths Biology Notes Physics Notes Chemistry Notes
To get study material, exam alerts and news, join our Whatsapp Channel.

