Class 9 Maths Linear Equations in Two Variables – Get here the Notes for Class 9 Linear Equations in Two Variables. Candidates who are ambitious to qualify the Class 9 with good score can check this article for Notes. This is possible only when you have the best CBSE Class 9 Maths study material and a smart preparation plan. To assist you with that, we are here with notes. Hope these notes will helps you understand the important topics and remember the key points for exam point of view. Below we provided the Notes of Class 9 Maths for topic Linear Equations in Two Variables.
- Class: 9th
- Subject: Maths
- Topic: Linear Equations in Two Variables
- Resource: Notes
CBSE Notes Class 9 Maths Linear Equations in Two Variables
Candidates who are pursuing in Class 9 are advised to revise the notes from this post. With the help of Notes, candidates can plan their Strategy for particular weaker section of the subject and study hard. So, go ahead and check the Important Notes for Class 9 Maths Linear Equations in Two Variables from this article.
LINEAR EQUATION IN TWO VARIABLES
An equation of the form ax + by + c = 0 where a, b, c are real numbers and x, y are variables, is called a linear equation in two variables.
Here ‘a’ is called coefficient of x, ‘b’ is called coefficients of y and c is called constant term.
Eg. 6x + 2y + 5 = 0, 5x – 2y + 3 = 0 etc.
SOLUTIONS OF LINEAR EQUATION
The value of the variable which when substituted for the variable in the equation satisfies the equation i.e. L.H.S. and R.H.S. of the equation becomes equal, is called the solution or root of the equation.
RULES FOR SOLVING AN EQUATION
(i) Same quantity can be added to both sides of an equation without changing the equality.
(ii) Same quantity can be subtracted from both sides of an equation without changing the equality.
(iii) Both sides of an equation may be multiplied by a same non-zero number without changing the equality.
(iv) Both sides of an equation may be divided by a same non-zero number without changing the equality.
A LINEAR EQUATION EN TWO VARIABLES
HAS INFINITELY MANY SOLUTIONS
We can get many many solutions in the following way.
Pick a value of your choice for x (say x = 2) in 2x + 3y = 12. then the equation reduces to 4+3y = 12, which is a linear equation in one variable. On solving this, you get y = 8/3. So (2, 8/3) is another solution of 2x + 3y = 12. Similarly, choosing x = —5, you find that the equation becomes — 10 + 3y = 12. This gives y =22/3. So, (-5, 22/3) is another solution of 2x + 3y = 12. So there is no end to different solutions of a linear equation in two variables.
Note : An easy way of getting a solution is to take x = 0 and get the corresponding value of y. Similarly, we can put y =0 and obtain the corresponding value of x.
GRAPH OF LINEAR EQUATIONS
The graph of an equation in x and y is the set of all points whose coordinates satisfy the equation :
In order to draw the graph of a linear equation ax + by + c = 0 may follow the following algorithm.
Step 1: Obtain the linear equation ax + by+ c = 0
Step 2 : Express yin terms of x i.e. y = -((ax + b)/c))
Step 3 : Put any two or three values for x and calculate the corresponding values of y from the expression values of y from the expression obtained in step 2. Let we get points as (α1, β1), (α2, β2), (α3, β3)
Step 4 : Plot points (α1, β1), (α2, β2), (α3, β3) on graph paper.
Step 5 : Join the points marked in step 4 to obtain. The line obtained is the graph of the equation ax+by+c= 0
Note : (i) The reason that a degree one polynomial equation ax + by + c = 0 is called a linear equation is that its geometrical representation is a straight line.
(ii) The graph of the equation of the form y = kx is a line which always passes through the origin.
EQUATIONS OF LINES PARALLEL TO THE X— AXIS AND Y— AXIS
Every point on the x – axis is of the form (x, 0). The equation of the x – axis is given byy 0. Note that y =0 can be expressed as 0. x + 1.)) 0.
Similarly, observe that the equation of they – axis is given by x = 0.
Consider the equation x -2 = 0. If this is treated as an equation in one variable x only, then it has the unique solution x= 2, which is a point on the number line.
An equation in two variables, x -2 = 0 is represented by the line AB in the graph in below given fig.
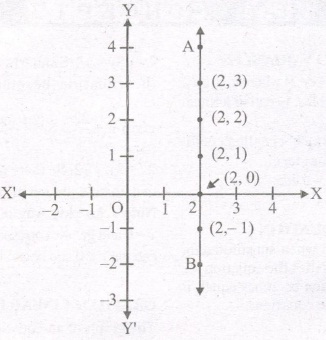
Note : (i) The graph ofx = a is a straight line parallel to they – axis
(ii) The graph ofy = a is a straight line parallel to thex – axis.
Class 9 Key Points, Important Questions & Practice Papers
Hope these notes helped you in your schools exam preparation. Candidates can also check out the Key Points, Important Questions & Practice Papers for various Subjects for Class 9 in both Hindi and English language form the link below.
| Class 9 Maths | कक्षा 9 गणित |
| Class 9 Science | कक्षा 9 सामाजिक विज्ञान |
| Class 9 English | |
| Class 9 Social Science |
Class 9 NCERT Solutions
Candidates who are studying in Class 9 can also check Class 9 NCERT Solutions from here. This will help the candidates to know the solutions for all subjects covered in Class 9th. Candidates can click on the subject wise link to get the same. Class 9 Chapter-wise, detailed solutions to the questions of the NCERT textbooks are provided with the objective of helping students compare their answers with the sample answers.
Class 9 Mock Test / Practice
Mock test are the practice test or you can say the blue print of the main exam. Before appearing in the main examination, candidates must try mock test as it helps the students learn from their mistakes. With the help of Class 9 Mock Test / Practice, candidates can also get an idea about the pattern and marking scheme of that examination. For the sake of the candidates we are providing Class 9 Mock Test / Practice links below.
Class 9 Exemplar Questions
Exemplar Questions Class 9 is a very important resource for students preparing for the Examination. Here we have provided Exemplar Problems Solutions along with NCERT Exemplar Problems Class 9. Question from very important topics is covered by Exemplar Questions for Class 9.
