Class 9 Maths Volume and Surface Area – Get here the Notes for Class 9 Volume and Surface Area . Candidates who are ambitious to qualify the Class 9 with good score can check this article for Notes. This is possible only when you have the best CBSE Class 9 Maths study material and a smart preparation plan. To assist you with that, we are here with notes. Hope these notes will helps you understand the important topics and remember the key points for exam point of view. Below we provided the Notes of Class 9 Maths for topic Volume and Surface Area.
- Class: 9th
- Subject: Maths
- Topic: Volume and Surface Area
- Resource: Notes
CBSE Notes Class 9 Maths Volume and Surface Area
Candidates who are pursuing in Class 9 are advised to revise the notes from this post. With the help of Notes, candidates can plan their Strategy for particular weaker section of the subject and study hard. So, go ahead and check the Important Notes for Class 9 Maths Volume and Surface Area from this article.
SOLIDS : The bodies occupying space (i.e. have 3-dimension) are called solids such as a cuboid, a cube, a cylinder, a cone, a sphere etc.
VOLUME (CAPACITY) OFA SOLID: The measure of space occupied by a solid-body is called its volume. The units of volume are cubic centimeters (written as cm3) or cubic meters (written as m3).
CUBOID: A solid bounded by six rectangular faces is called a cuboid.
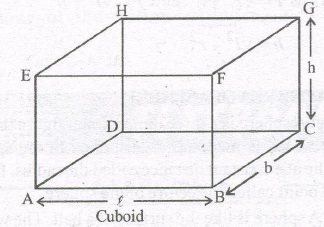
In the given figure, ABCDEFGH is a cuboid whose
(i) 6 faces are :
ABCD, EFGH, ABFE, CDHQ ADHE, and BCGF Out of these, the four faces namely ABFE, DCGH, ADHE and BCGF are called lateral faces of the cuboid.
(ii) 12 edges are :
AB, BC, CD, DA, EF, FG GH, HE, CG BF, AE and DH
(iii) 8 vertices are :
A, B, C, D, E, F, and H.
Remark : A rectangular room is in the form of a cuboid and its 4 walls are its lateral surfaces.
Cube : A cuboid whose length, breadth and height are all equal, is called a cube.
A cube has 6 faces, each face is square, 12 edges, all edges are of equal lengths and 8 vertices.
SURFACE AREA OF A CUBOID:
Let us consider a cuboid of length = 1 units
Breadth = b units and height = h units
Then we have :
(i) Total surface area of the cuboid
=2(l * b + b * h + h * l) sq. units
(ii) Lateral surface area of the cuboid
= [2 (1 + b)* h] sq. units
(iii) Area of four walls of a room = [2 (1 + b)* h] sq. units.
= (Perimeter of the base * height) sq. units
(iv) Surface area of four walls and ceiling of a room
= lateral surface area of the room + surface area of ceiling
=2(1+b)*h+l*b
(v) Diagonal of the cuboid = √l2 + b2 + h2
SURFACE AREA OF A CUBE : Consider a cube of edge a unit.
(i) The Total surface area of the cube = 6a2 sq. units
(ii) Lateral surface area of the cube = 4a2 sq. units.
(iii) The diagonal of the cube = √3 a units.
SURFACE AREA OF THE RIGHT CIRCULAR CYLINDER
Cylinder: Solids like circular pillars, circular pipes, circular pencils, road rollers and gas cylinders etc. are said to be in cylindrical shapes.
Curved surface area of the cylinder
= Area of the rectangular sheet
= length * breadth
= Perimeter of the base of the cylinder * height
= 2πr * h
Therefore, curved surface area of a cylinder = 2πrh
Total surface area of the cylinder =2πrh + 2πr2
So total area of the cylinder=2πr(r + h)
Remark : Value of TE approximately equal to 22 / 7 or 3.14.
APPLICATION:
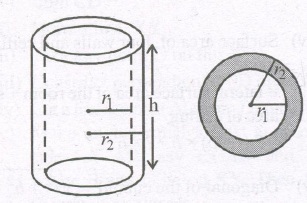
If a cylinder is a hollow cylinder whose inner radius is r1 and outer radius r2 and height h then
Total surface area of the cylinder
= 2πr1h + 2πr2h + 2π(r22 – r21)
= 2π(r1 + r2)h + 2π (r2 + r1) (r2 – r1)
= 2π(r1 + r2) [h + r2 – r1]
SURFACE AREA OF A RIGHT CIRCULAR CONE
RIGHT CIRCULAR CONE
A figure generated by rotating a right triangle about a perpendicular side is called the right circular cone.
SURFACE AREA OF A RIGHT CIRCULAR CONE:
curved surface area of a cone = 1 / 2 * l * 2πr = πrl
where r is base radius and l its slant height
Total surface area of the right circular cone
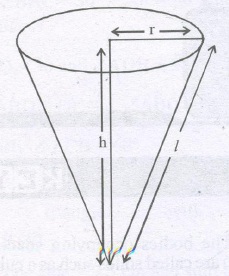
= curved surface area + Area of the base
= πrl + πr2 = πr(l + r)
Note : l2 = r2 + h2
By applying Pythagorus
Theorem, here h is the height of the cone.
Thus l = √r2 + h2 and r = √l2 – h2
h = √l2 + r2
SURFACE AREA OF A SPHERE
Sphere: A sphere is a three dimensional figure (solid figure) which is made up of all points in the space which lie at a constant distance called the radius, from a fixed point called the centre of the sphere.
Note : A sphere is like the surface of a ball. The word solid sphere is used for the solid whose surface is a sphere.
Surface area of a sphere: The surface area of a sphere of radius r = 4 x area of a circle of radius r = 4 * πr2
= 4πr2
Surface area ofa hemisphere = 2πr2
Total surface area of a hemisphere = 2πr2 + πr2
= 3πr2
Total surface area of a hollow hemisphere with inner and outer radius r1 and r2 respectively
= 2πr21 + 2πr22 + π(r22 — r21)
= 2π(r21 + r22) + π(r22 —r21)
VOLUMES
VOLUME OF A CUBOID :
Volume : Solid objects occupy space.
The measure of this occupied space is called volume of the object.
Capacity of a container : The capacity of an object is the volume of the substance its interior can accommodate.
The unit of measurement of either of the two is cubic unit.
Volume of a cuboid : Volume of a cuboid =Area of the base * height V=l * b * h
So, volume of a cuboid = base area * height = length * breadth * height
Volume of a cube : Volume of a cube = edge * edge * edge = a3
where a = edge of the cube
VOLUME OF A CYLINDER
Volume of a cylinder = πr2h
volume of the hollow cylinder πr22h — πr21h
= π(r22 – r21)h
VOLUME OF A RIGHT CIRCULAR CONE
volume of a cone = 1 / 3 πr2h, where r is the base radius
and h is the height of the cone.
VOLUME OF A SPHERE
volume of a sphere the sphere = 4 / 3 πr3, where r is the radius of the sphere.
Volume of a hemisphere = 2 / 3 πr3
APPLICATION : Volume of the material of a hollow sphere with inner and outer radii r1 and r2respectively
= 4 / 3 πr32 – 4 / 3 πr31 = 4 / 3π(r32 – r31)
Volume of the material of a hemisphere with inner and
outer radius r1 and r2 respectively = 2 / 3π(r32 – r31)
Class 9 Key Points, Important Questions & Practice Papers
Hope these notes helped you in your schools exam preparation. Candidates can also check out the Key Points, Important Questions & Practice Papers for various Subjects for Class 9 in both Hindi and English language form the link below.
| Class 9 Maths | कक्षा 9 गणित |
| Class 9 Science | कक्षा 9 सामाजिक विज्ञान |
| Class 9 English | |
| Class 9 Social Science |
Class 9 NCERT Solutions
Candidates who are studying in Class 9 can also check Class 9 NCERT Solutions from here. This will help the candidates to know the solutions for all subjects covered in Class 9th. Candidates can click on the subject wise link to get the same. Class 9 Chapter-wise, detailed solutions to the questions of the NCERT textbooks are provided with the objective of helping students compare their answers with the sample answers.
Class 9 Mock Test / Practice
Mock test are the practice test or you can say the blue print of the main exam. Before appearing in the main examination, candidates must try mock test as it helps the students learn from their mistakes. With the help of Class 9 Mock Test / Practice, candidates can also get an idea about the pattern and marking scheme of that examination. For the sake of the candidates we are providing Class 9 Mock Test / Practice links below.
Class 9 Exemplar Questions
Exemplar Questions Class 9 is a very important resource for students preparing for the Examination. Here we have provided Exemplar Problems Solutions along with NCERT Exemplar Problems Class 9. Question from very important topics is covered by Exemplar Questions for Class 9.
CBSE Class 9 Maths Notes Science Notes Social Science Notes English Notes
To get study material, exam alerts and news, join our Whatsapp Channel.


