CBSE Class 11 Maths Binomial Theorem and Mathematical Induction – Get here the Notes for Class 11 Binomial Theorem and Mathematical Induction. Candidates who are ambitious to qualify the Class 11 with good score can check this article for Notes. This is possible only when you have the best CBSE Class 11 Maths study material and a smart preparation plan. To assist you with that, we are here with notes. Hope these notes will helps you understand the important topics and remember the key points for exam point of view. Below we provided the Notes of CBSE Class 11 Maths for topic Binomial Theorem and Mathematical Induction.
- Class: 11th
- Subject: Maths
- Topic: Binomial Theorem and Mathematical Induction
- Resource: Notes
CBSE Notes Class 11 Maths Binomial Theorem and Mathematical Induction
Candidates who are pursuing in CBSE Class 11 Maths are advised to revise the notes from this post. With the help of Notes, candidates can plan their Strategy for particular weaker section of the subject and study hard. So, go ahead and check the Important Notes for CBSE Class 11 Maths Binomial Theorem and Mathematical Induction from this article.
Binomial Theorem for Positive Integer
If n is any positive integer, then
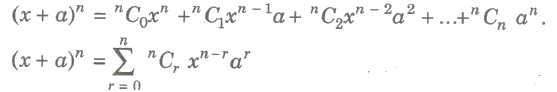
This is called binomial theorem.
Here, nC0, nC1, nC2, … , nno are called binomial coefficients and
nCr = n! / r!(n – r)! for 0 ≤ r ≤ n.
Properties of Binomial Theorem for Positive Integer
(i) Total number of terms in the expansion of (x + a)n is (n + 1).
(ii) The sum of the indices of x and a in each term is n.
(iii) The above expansion is also true when x and a are complex numbers.
(iv) The coefficient of terms equidistant from the beginning and the end are equal. These coefficients are known as the binomial coefficients and
nCr = nCn – r, r = 0,1,2,…,n.
(v) General term in the expansion of (x + c)n is given by
Tr + 1 = nCrxn – r ar.
(vi) The values of the binomial coefficients steadily increase to maximum and then steadily decrease .

(vii)
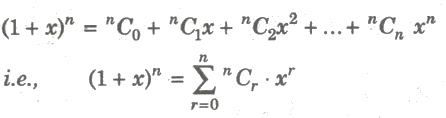
(viii)
(ix) The coefficient of xr in the expansion of (1+ x)n is nCr.
(x)
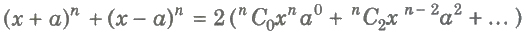
(xi) (a)
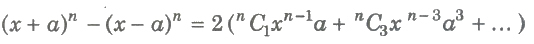
(b)
(xii) (a) If n is odd, then (x + a)n + (x – a)n and (x + a)n – (x – a)n both have the same number of terms equal to (n +1 / 2).
(b) If n is even, then (x + a)n + (x – a)n has (n +1 / 2) terms. and (x + a)n – (x – a)n has (n / 2) terms.

(xiii) In the binomial expansion of (x + a)n, the r th term from the end is (n – r + 2)th term from the beginning.
(xiv) If n is a positive integer, then number of terms in (x + y + z)n is (n + l)(n + 2) / 2.
Middle term in the Expansion of (1 + x)n
(i) It n is even, then in the expansion of (x + a)n, the middle term is (n/2 + 1)th terms.
(ii) If n is odd, then in the expansion of (x + a)n, the middle terms are (n + 1) / 2 th term and (n + 3) / 2 th term.
Greatest Coefficient
(i) If n is even, then in (x + a)n, the greatest coefficient is nCn / 2
(ii) Ifn is odd, then in (x + a)n, the greatest coefficient is nCn – 1 / 2 or nCn + 1 / 2 both being equal.
Greatest Term
In the expansion of (x + a)n
(i) If n + 1 / x/a + 1 is an integer = p (say), then greatest term is Tp == Tp + 1.
(ii) If n + 1 / x/a + 1 is not an integer with m as integral part of n + 1 / x/a + 1, then Tm + 1. is the greatest term.
Important Results on Binomial Coefficients


Divisibility Problems
From the expansion, (1+ x)n = 1+ nC1x + nC1x2+ … +nCnxn
We can conclude that,
(i) (1+ x)n – 1 = nC1x + nC1x2+ … +nCnxn is divisible by x i.e., it is multiple of x.
(1+ x)n – 1 = M(x)
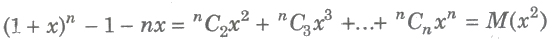
(ii)
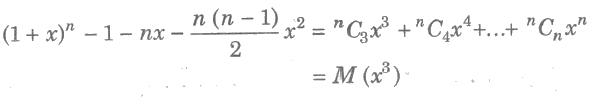
(iii)
Multinomial theorem
For any n ∈ N,

(i)
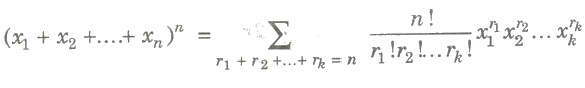
(ii)
(iii) The general term in the above expansion is
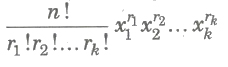

(iv)The greatest coefficient in the expansion of (x1 + x2 + … + xm)n is where q and r are the quotient and remainder respectively, when n is divided by m.
(v) Number of non-negative integral solutions of x1 + x2 + … + xn = n is n + r – 1Cr – 1
R-f Factor Relations
Here, we are going to discuss problem involving (√A + B)sup>n = I + f, Where I and n are positive integers.
0 le; f le; 1, |A – B2| = k and |√A – B| < 1
Binomial Theorem for any Index
If n is any rational number, then
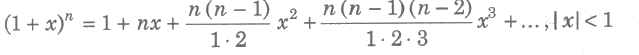
(i) If in the above expansion, n is any positive integer, then the series in RHS is finite otherwise infinite.
(ii) General term in the expansion of (1 + x)n is Tr + 1 = n(n – 1)(n – 2)… [n – (r – 1)] / r! * xr
(iii) Expansion of (x + a)n for any rational index
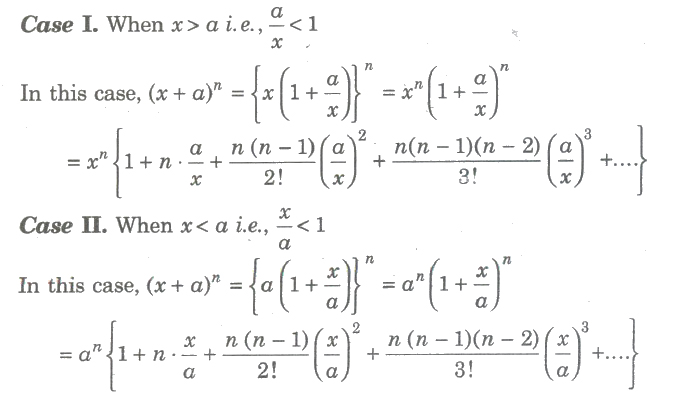

(vii) (1 + x)– 1 = 1 – x + x2 – x3 + …∞
(viii) (1 – x)– 1 = 1 + x + x2 + x3 + …∞
(ix) (1 + x)– 2 = 1 – 2x + 3x2 – 4x3 + …∞
(x) (1 – x)– 2 = 1 + 2x + 3x2 – 4x3 + …∞
(xi) (1 + x)– 3 = 1 – 3x + 6x2 – …∞
(xii) (1 – x)– 3 = 1 + 3x + 6x2 – …∞
(xiii) (1 + x)n = 1 + nx, if x2, x3,… are all very small as compared to x.
Important Results
(i) Coefficient of xm in the expansion of (axp + b / xq)n is the coefficient of Tr + l where r = np – m / p + q
(ii) The term independent of x in the expansion of axp + b / xq)n is the coefficient of Tr + l where r = np / p + q
(iii) If the coefficient of rth, (r + l)th and (r + 2)th term of (1 + x)n are in AP, then n2 – (4r+1) n + 4r2 = 2
(iv) In the expansion of (x + a)n
Tr + 1 / Tr = n – r + 1 / r * a / x
(v) (a) The coefficient of xn – 1 in the expansion of
(x – l)(x – 2) ….(x – n) = – n (n + l) / 2
(b) The coefficient of xn – 1 in the expansion of
(x + l)(x + 2) ….(x + n) = n (n + l) / 2
(vi) If the coefficient of pth and qth terms in the expansion of (1 + x)n are equal, then p + q = n + 2
(vii) If the coefficients of xr and xr + 1 in the expansion of a + x / b)n are equal, then
n = (r + 1)(ab + 1) – 1
(viii) The number of term in the expansion of (x1 + x2 + … + xr)n is n + r – 1C r – 1.
(ix) If n is a positive integer and a1, a2, … , am ∈ C, then the coefficient of xr in the expansion of (a1 + a2x + a3x2 +… + amxm – 1)n is
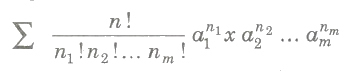
(x) For |x| < 1,
(a) 1 + x + x2 + x3+ … + ∞ = 1 / 1 – x
(b) 1 + 2x + 3x2 + … + ∞ = 1 / (1 – x)2
(xi) Total number of terms in the expansion of (a + b + c + d)n is (n + l)(n + 2)(n + 3) / 6.
Important Points to be Remembered
(i) If n is a positive integer, then (1 + x)n contains (n +1) terms i.e., a finite number of terms. When n is general exponent, then the expansion of (1 + x)n contains infinitely many terms.
(ii) When n is a positive integer, the expansion of (l + x)n is valid for all values of x. If n is general exponent, the expansion of (i + x)n is valid for the values of x satisfying the condition |x| < 1.
Class 11 Key Points, Important Questions & Practice Papers
Hope these notes helped you in your schools exam preparation. Candidates can also check out the Key Points, Important Questions & Practice Papers for various Subjects for Class 11 in both Hindi and English language form the link below.
Class 11 NCERT Solutions
Candidates who are studying in Class 11 can also check Class 11 NCERT Solutions from here. This will help the candidates to know the solutions for all subjects covered in Class 11th. Candidates can click on the subject wise link to get the same. Class 11 Chapter-wise, detailed solutions to the questions of the NCERT textbooks are provided with the objective of helping students compare their answers with the sample answers.
Class 11 Mock Test / Practice
Mock test are the practice test or you can say the blue print of the main exam. Before appearing in the main examination, candidates must try mock test as it helps the students learn from their mistakes. With the help of Class 11 Mock Test / Practice, candidates can also get an idea about the pattern and marking scheme of that examination. For the sake of the candidates we are providing Class 11 Mock Test / Practice links below.
Class 11 Exemplar Questions
Exemplar Questions Class 11 is a very important resource for students preparing for the Examination. Here we have provided Exemplar Problems Solutions along with NCERT Exemplar Problems Class 11. Question from very important topics is covered by Exemplar Questions for Class 11.
CBSE Notes for Class 11 Maths Biology Notes Physics Notes Chemistry Notes
To get study material, exam alerts and news, join our Whatsapp Channel.

