CBSE Class 11 Maths Permutations and Combinations – Get here the Notes for Class 11 Permutations and Combinations. Candidates who are ambitious to qualify the Class 11 with good score can check this article for Notes. This is possible only when you have the best CBSE Class 11 Maths study material and a smart preparation plan. To assist you with that, we are here with notes. Hope these notes will helps you understand the important topics and remember the key points for exam point of view. Below we provided the Notes of CBSE Class 11 Maths for topic Permutations and Combinations.
- Class: 11th
- Subject: Maths
- Topic: Permutations and Combinations
- Resource: Notes
CBSE Notes Class 11 Maths Permutations and Combinations
Candidates who are pursuing in CBSE Class 11 Maths are advised to revise the notes from this post. With the help of Notes, candidates can plan their Strategy for particular weaker section of the subject and study hard. So, go ahead and check the Important Notes for CBSE Class 11 Maths Maths Permutations and Combinations from this article.
Fundamental Principles of Counting
1. Multiplication Principle
If first operation can be performed in m ways and then a second operation can be performed in n ways. Then, the two operations taken together can be performed in mn ways. This can be extended to any finite number of operations.
2. Addition Principle
If first operation can be performed in m ways and another operation, which is independent of the first, can be performed in n ways. Then, either of the two operations can be performed in m + n ways. This can be extended to any finite number of exclusive events.
Factorial
For any natural number n, we define factorial as n ! or n = n(n – 1)(n – 2) … 3 x 2 x 1 and 0!= 1!= 1
Permutation
Each of the different arrangement which can be made by taking some or all of a number of things is called a permutation.
Mathematically The number of ways of arranging n distinct objects in a row taking r (0 ≤ r ≤ n) at a time is denoted by P(n ,r) or npr
Properties of Permutation
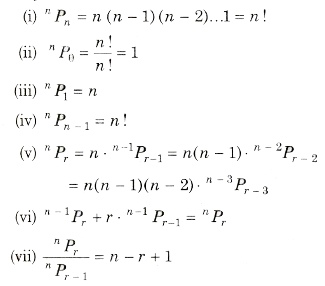
Important Results on’Permutation
- The number of permutations of n different things taken r at a time, allowing repetitions is nr.
- The number of permutations of n different things taken all at a time is nPn= n! .
- The number of permutations of n things taken all at a time, in which p are alike of one kind, q are alike of second kind and r are alike of third kind and rest are different is n!/(p!q!r!)
- The number of permutations of n things of which p1 are alike of one kind p2 are alike of second kind, p3 are alike of third kind,…, Pr are alike of rth kind such that p1 + p2 + p3 +…+pr = n is n!/P1!P2!P3!….Pr!
- Number of permutations of n different things taken r at a time,
when a particular thing is to be included in each arrangement is r.n – 1Pr – 1.
when a particular thing is always excluded, then number of arrangements = n – 1Pr - Number of permutations of n different things taken all at a time, when m specified things always come together is m!(n – m + 1)!.
- Number of permutations of n different things taken all at a time, when m specified things never come together is n! – m! x (n – m + 1)!.
Division into Groups
(i) The number of ways in which (m + n) different things can be divided into two groups which contain m and n things respectively [(m + n)!/m ! n !].
This can be extended to (m + n + p) different things divided into three groups of m, n, p things respectively [(m + n + p)!/m!n! p!].
(ii) The number of ways of dividing 2n different elements into two groups of n objects each is [(2n)!/(n!)2] , when the distinction can be made between the groups, i.e., if the order of group is important. This can be extended to 3n different elements into 3 groups is [(3n)!/((n!)3].
(iii) The number of ways of dividing 2n different elements into two groups of n object when no distinction can be made between the groups i.e., order of the group is not important is
[(2n)!/2!(n!)2].
This can be extended to 3n different elements into 3 groups is
[(3n)!/3!(n!)3].
The number of ways in which mn different things can be divided equally it into m groups, if order of the group is not important is
[(mn)!/(n!)m m!].
(v) If the order of the group is important, then number of ways of dividing mn different things equally into m distinct groups is mn
[(mn)!/(n!)m]
(vi) The number of ways of dividing n different things into r groups is
[rn — rC1(r — 1)n + rC2(r — 2)n — rC3(r – 3)n + …]
.
(vii) The number of ways of dividing n different things into r groups taking into account the order of the groups and also the order of things in each group is
n+r-1Pn = r(r + l)(r + 2) … (r + n – 1).
(viii) The number of ways of dividing n identical things among r persons such that each gets 1, 2, 3, … or k things is the coefficient of xn – r in the expansion of (1 + x + x2 + … + Xk-1)r.
Circular Permutation
In a circular permutation, firstly we fix the position of one of the objects and then arrange the other objects in all possible ways.
(i) Number of circular permutations at a time is (n -1)!. If clockwise taken as different. of n and different things taken anti-clockwise orders all are
(ii) Number of circular permutations of n different things taken all at a time, when clockwise or anti-clockwise order is not different 1/2(n – 1)!.
(iii) Number of circular permutations of n different things taken r at a time, when clockwise or anti-clockwise orders are take as different is
nPr/r.
(iv) Number of circular permutations of n different things taken r at a time, when clockwise or anti-clockwise orders are not different is
nPr/2r.
(v) If we mark numbers 1 to n on chairs in a round table, then n persons sitting around table is n!.
Combination
Each of the different groups or selections which can be made by some or all of a number of given things without reference to the order of the
things in each group is called a combination.
Mathematically The number of combinations of n different things taken r at a time is
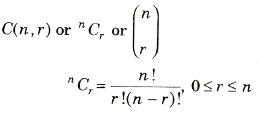
Properties of Combination

Important Results on Combination
- The number of combinations of n different things taken r at a time allowing repetitions is n + r – 1Cr
- The number of ways of dividing n identical things among r persons such that each one gets at least one is n – 1Cr – 1.
- The total number of combinations of n different objects taken r at a time in which
(a) m particular objects are excluded = n – mCr
(b) m particular objects are included = n – mCr – 1 - The total number of ways of dividing n identical items among r persons, each one of whom can receive 0, 1, 2 or more items (≤ n) is n + r – 1Cr – 1
- The number of ways in which n identical items can be divided into r groups so that no group contains less than in items and more than k(m < k) is coefficient of xn in the expansion of (xm + xm + 1 +….+ xk)r.
- The total number of ways of selection of some or all of n things at a time is nC1 + nC2 +….+ nn1 = 2n — 1.
- The number of selections of r objects out of n identical objects is 1.
- Total number of selections of zero or more objects from n identical objects is n + 1.
Important Points to be Remembered
1. Function
(i) If a set A has m elements and set B has n elements, then
(a) number of functions from A to B is nm
(b) number of one-one function from A to B is nPm, m ≤ n.
(c) number of onto functions from A to B is nm — nC1(n — 1)m + nC2(n — 2)m…..; m ≤ n.
(d) number of increasing (decreasing) functions from A to B is nCm, m ≤ n.
(e) number of non-increasing (non-decreasing) functions from A to B is m + n – 1Cm .
(f) number of bijective (one-one onto) functions from A to B is n !, if m = n.
(ii) Number of permutations of n different objects taken r at a time in which m particular objects are always
(a) excluded = n – mPr
(b) included = n – mPr – m x r!
2. Geometry
- Given, n distinct points in the plane, no three of which are collinear, then the number of line segments formed = nC2.
- Given. ii distinct paints in the p)ane. in which m are collinear (m ≥ 3), then the number of line segments is (nC2 – mC2) + 1.
- Given, n distinct points in the plane, no three of which are collinear, then the number of triangle formed = nC3
- Given, n distinct points in a plane, in which m are collinear (m ≥ 3), then the number of triangle formed = nC3 — mC3
- The number of diagonals in a n-sided closed polygon = nC2 — n.
- Given, n points on the circumference of a circle, then
(a) number of straight lines = nC2
(b) number of triangles = nC3
(c) number of quadrilaterals = nC4 - Number of rectangles of any size in a square of n x n is and number of square of any size is .
- In a rectangle of n x p (n < p), numbers of rectangles of any size is np/4 (n + 1) (p + 1) and number of squares of any size is
- Suppose n straight lines are drawn in the plane such that no two lines are parallel and no three lines are concurrent, then number of parts which these divides the plane is equal to 1 +∑ n.
3. Prime Factors
Any natural number > 1, can be expressed as product of primes.
- Let n = p1α1 p2α2 p3α3 …. prαr, where
- pi, i = 1, 2, 3, … , r, are prime numbers.
- αi, i = 1, 2, 3, … , r, are positive integers.
- Number of distinct positive integral divisors of n is (α1 + 1)(α2 + 1)(α3 + 1) … (αr + 1).
- Sum of distinct positive integral divisors of n is
- Total number of divisors of n (excluding 1 and n), is (α1 + 1)(α2 + 1)(α3 + 1) … (αr + 1) – 2.
- Total number of divisors of n (excluding 1 or n), is (α1 + 1)(α2 + 1)(α3 + 1) … (αr + 1) – 1.
- The number of ways in which n can be resolved as a product of two factors is
(a) 1/2(α1 + 1)(α2 + 1)(α3 + 1) … (αr + 1) if n is not a perfect square.
(b) 1/2[(α1 + 1)(α2 + 1)(α3 + 1) … (αr + 1) + 1], if n is a perfect square. - The number of ways in which n can be resolved into two factors which are prime to each other is 2r – 1, where r is the number of different factors in n.
- If p is prime and pr divides n!, then
4. Integral Solutions
- The number of integral solutions of x1+ x2 +….+ xr = n, where x1, x2, … xr ≥ 0 is n + r – 1Cr – 1.
- Number of integral solutions of x1+ x2 +….+ xr = n, where x1, x2, … xr ≥ 1 is n – 1Cr – 1
5. Sum of Digits
- Sum of the numbers formed by taking all the given n digits = (Sum of all the n digits) x (n — 1)! x (111… 1)n times.
- The sum of all digits in the unit place of all numbers formed with the help of ai , a2, , an all at a time is (n — 1)!(a1 + a1 + …. + an).
- The sum of all digits of numbers that can be formed by using the digits a1, a2,… , an (repetition of digits is not allowed (n — 1)! (a1 + a1 + … + an)((10n – 1)/9)
6. Arrangements
- The number of ways in which m (one type of different things) and n (another type of different things) can be arranged in a row so that all the second type of things come together is n !(m + 1)!.
- The number of ways in which m (one type of different things) and n (another type of different things) can be arranged in row so that no two things of the same type come together is 2 x m! n!
- The number of ways in which m (one type of different things) and n (another type of different things) (m ≥ n), can be arranged in a circle so that no two things of second type come together (m – 1)! mPn and when things of second type come together = m! n!
- The number of ways in which m things of one type and n things of another type (all different) can be arranged in the form of a garland so that all the second type of things come together, is m! n!/2 and if no things of second type come together is, [((m – 1)!mPn)/2]
7. Dearrangements
If n distinct objects are arranged in a row, then the number of ways in which they can be rearranged so that no one of them occupies the place assigned to it is

8. Selection
- The total number of ways in which it is possible to make a selection by taking some or all the given n different objects is
nC1 + nC2 + …. + nCn = 2n – 1 - If there are m items of one kind, n items of another kind and so on. Then, the number of ways of choosing r items out of these items = coefficient of xr in
(1 + x + x2 + …. + xm)(1 + x + x2 + …. + xn) - If there are m items of one kind, n items of another kind and so on. Then, the number of ways of choosing r items out of these items such that at least one item of each kind is included in every selection = coefficient of xr in
(x + x2 + …. + xm)(x + x2 + …. + xn)…. - The number of ways of selecting r items from a group of n items in which p are identical, is
n – PCr + n – PCr – 1+ n – PCr – 2 + … + n – PC0, if r ≤ P and n – PCr + n – PCr – 1+ n – PCr – 2 + … + n – PCr – p, if r > P - The number of ways in which n identical things can be distributed into r different groups is n + r – lCr – 1, or n – 1Cr – 1 according as blanks groups are or are not admissible.
- The number of ways of answering one or more of n questions is 2n – 1.
- The number of ways of answering one or more n questions when each question has an alternative = 2n
- n! + 1 is not divisible by any natural number between 2 and n.
- If there are 1 objects of one kind, m objects of second kind, n objects of third kind and so on. Then, the number of possible arrangements of r objects out of these objects = Coefficient of xr in the expansion of
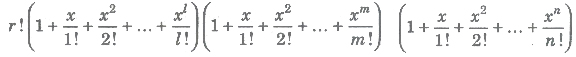
Class 11 Key Points, Important Questions & Practice Papers
Hope these notes helped you in your schools exam preparation. Candidates can also check out the Key Points, Important Questions & Practice Papers for various Subjects for Class 11 in both Hindi and English language form the link below.
Class 11 NCERT Solutions
Candidates who are studying in Class 11 can also check Class 11 NCERT Solutions from here. This will help the candidates to know the solutions for all subjects covered in Class 11th. Candidates can click on the subject wise link to get the same. Class 11 Chapter-wise, detailed solutions to the questions of the NCERT textbooks are provided with the objective of helping students compare their answers with the sample answers.
Class 11 Mock Test / Practice
Mock test are the practice test or you can say the blue print of the main exam. Before appearing in the main examination, candidates must try mock test as it helps the students learn from their mistakes. With the help of Class 11 Mock Test / Practice, candidates can also get an idea about the pattern and marking scheme of that examination. For the sake of the candidates we are providing Class 11 Mock Test / Practice links below.
Class 11 Exemplar Questions
Exemplar Questions Class 11 is a very important resource for students preparing for the Examination. Here we have provided Exemplar Problems Solutions along with NCERT Exemplar Problems Class 11. Question from very important topics is covered by Exemplar Questions for Class 11.
CBSE Notes for Class 11 Maths Biology Notes Physics Notes Chemistry Notes
To get study material, exam alerts and news, join our Whatsapp Channel.

