Class 10 Maths Surface Areas and Volumes – Get here the Notes for Class 10 Maths Surface Areas and Volumes. Candidates who are ambitious to qualify the Class 10 with good score can check this article for Notes. This is possible only when you have the best CBSE Class 10 Maths study material and a smart preparation plan. To assist you with that, we are here with notes. Hope these notes will help you understand the important topics and remember the key points for exam point of view. Below we provided the Notes of Class 10 Maths for topic Surface Areas and Volumes.
- Class: 10th
- Subject: Maths
- Topic: Surface Areas and Volumes
- Resource: Notes
CBSE Notes Class 10 Maths Surface Areas and Volumes
Candidates who are pursuing in Class 10 are advised to revise the notes from this post. With the help of Notes, candidates can plan their Strategy for particular weaker section of the subject and study hard. So, go ahead and check the Important Notes for CBSE Class 10 Maths Surface Areas and Volumes from this article.
(A) RIGHT CIRCULAR CYLINDER:
A right circular cylinder is solid generated by the revolution of a rectangle about of its sides.
NOTE : If a paper, cylinder open at both the ends is cut along a vertical line on the curved surface and stretched on a plane surface, we obtain a rectangle of length i.e., 27πr and breadth= Height of cylinder h.
So, curved surface area (C.S.A) or lateral surface area = 2πr * height
Important Formula For Cylinder
1. C. S. A of cylinder = ( Perimeter of base) * Height = 2πrh
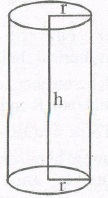
2. Area of each end of cylinder = 2πr2
3. Total surface area (including both circular ends) = 2πrh + 2πr2 = 27πr(h + r)
4. Volume of cylinder — πr2h = [(Area of base) * height]
Hollow Cylinder’s formulae e.g., (Rubber tubes pipes, etc.)
1. Volume of material = Exterior volume — Interior
volume = πR2h — πr2h = πh(R2 – r2)
2. C. S. A or L. S. A = external surface area + internal surface area
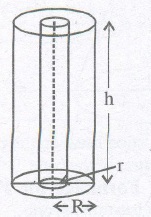
= 2πRh + 2πrh
3. T. S . A. of hollow cylinder = C. S. A+ 2 ( area of base ring )
= (2πRh + 2πrh) + 2(πR2 – πr2)
NOTE:
1. Two end faces of right circular cylinder are circles having each area = πr2
2. Mass of cylinder = Volume * density
3. When rectangular sheet of paper is rolled along its length , we get a cylinder whose base circumference is length of sheet and height is same as breadth of sheet.
(B) CONE
From figure, AO = height of cone and is denoted by ‘h’

OB = radius of the base of cone, AB = slant height of a cone (l)
Important Formula Of rt. Circular Cone :
1. Volume of cone = 1 / 3 πr2h
2 C. S. A or L. S. A=πrl where slant height
= l =√ r2 + hr2
3. T. S. A of cone = πrl + πr2
(C) FRUSTUM OF A CONE
FRUSTUM : A cone is cut by a plane parallel to the base of the cone,

then the portion between the plane and base is called frustum of the cone
Important Formulae for Frustum :
1. Volume of frustum of cone
= πh / 3[R2 + r2 + Rr] cubic unit
2. L. S. A or C. S. A = πl(R + r) Sq units where l2 = h2 + (R – r)2
3. T. S. A = πR2 + πr2 + πl(R + r) Sq. units.
(Area of base + Area of top + Area of lateral )
4. Slant height (l) = √h22 + (R – r)2
(D) IMPORTANT FORMULA FOR SPHERE AND HEW-SPHERE
(a) Surface area of sphere = 4πr2
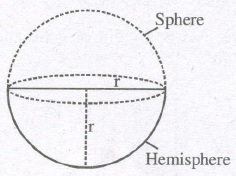
(b) Volume of sphere = 4 / 3 πr3
(c) Volume of hemisphere = 2 / 3 πr3
(d) C.S.A. of hemisphere = 2πr2
(e) Total surface area of Hemi-sphere = 2πr2 + πr2 =3πr2
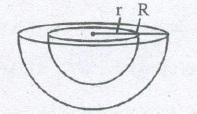
(E) IMPORTANT FORMULA FUR SPHERICAL SHELL/ HEMILSPHERICAL SHELL
(a) Outer surface area of spherical shell =4πR2
(b) Inner S.A. of spherical shell = 4πr2
(c) Total surface area of spherical shell = 4π(R2+ r2)
(d) Volume of spherical shell of external radius R and internal
radius ‘r’ = 4 / 3π(R3 – r3)
(e) Outer curved surface area hemispherical shell = 2πR2
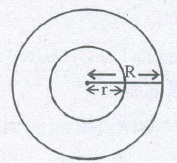
(f) Inner curved surface area of hemispherical shell = 2πr2
(g) Thick hemispherical bowl of external and internal radii R and r,
Total S.A. = π(3R2+ r2)
(h) Volume of hemispherical shell of external radius ‘R’ and internal radius ‘r’
= 2 / 3π(R3 — r2).
Class 10 Key Points, Important Questions & Practice Papers
Hope these notes helped you in your schools exam preparation. Candidates can also check out the Key Points, Important Questions & Practice Papers for various Subjects for Class 10 in both Hindi and English language form the link below.
| Class 10 Maths | कक्षा 10 गणित |
| Class 10 Science | कक्षा 10 विज्ञान |
| Class 10 Social Science | कक्षा 10 सामाजिक विज्ञान |
| Class 10 English |
Class 10 NCERT Solutions
Candidates who are studying in Class 10 can also check Class 10 NCERT Solutions from here. This will help the candidates to know the solutions for all subjects covered in Class 10th. Candidates can click on the subject wise link to get the same. Class 10 Chapter-wise, detailed solutions to the questions of the NCERT textbooks are provided with the objective of helping students compare their answers with the sample answers.
Class 10 Mock Test / Practice
Mock test are the practice test or you can say the blue print of the main exam. Before appearing in the main examination, candidates must try mock test as it helps the students learn from their mistakes. With the help of Class 10 Mock Test / Practice, candidates can also get an idea about the pattern and marking scheme of that examination. For the sake of the candidates we are providing Class 10 Mock Test / Practice links below.
Class 10 Exemplar Questions
Exemplar Questions Class 10 is a very important resource for students preparing for the Examination. Here we have provided Exemplar Problems Solutions along with NCERT Exemplar Problems Class 10. Question from very important topics is covered by Exemplar Questions for Class 10.
CBSE Class 10 Maths Notes Science Notes Social Science Notes English Notes
To get study material, exam alerts and news, join our Whatsapp Channel.

