CBSE Class 11 Maths Logarithm – Get here the Notes for Class 11 Logarithm. Candidates who are ambitious to qualify the Class 11 with good score can check this article for Notes. This is possible only when you have the best CBSE Class 11 Maths study material and a smart preparation plan. To assist you with that, we are here with notes. Hope these notes will helps you understand the important topics and remember the key points for exam point of view. Below we provided the Notes of CBSE Class 11 Maths for topic Logarithm.
- Class: 11th
- Subject: Maths
- Topic: Logarithm
- Resource: Notes
CBSE Notes Class 11 Maths Logarithm
Candidates who are pursuing in CBSE Class 11 Maths are advised to revise the notes from this post. With the help of Notes, candidates can plan their Strategy for particular weaker section of the subject and study hard. So, go ahead and check the Important Notes for CBSE Class 11 Maths Logarithm from this article.
If a is a positive real number other than 1 and ax = m, then x is called the logarithm of m to the base a, written as loga m. In loga m, m should be always positive.
(i) If m < 0, then loga m will be imaginary and if m = 0, then loga m will be meaningless.
(ii) loga m exists only, if m, a > 0 and a ≠ 1.
Types of Logarithms
1. Natural or Napier Logarithms
The logarithms with base ‘e’ (e = 2.718) are called natural logarithms.
e.g., loge x, loge 25 etc.
2. Common or Brigg’s Logarithms
The logarithm with base ’10’ are called common logarithm.
e.g., log10 x, log10 75 etc.
Note In a logarithmic expression when the base is not mentioned, it is taken as 10.
Characteristic and Mantissa of a Logarithm
The logarithm of positive real number ‘n’ consists of two parts.
1. The integral part is known as the characteristic. It is always an integer positive, negative or zero.
2. The decimal part is called as the mantissa. The mantissa is never negative and is always less than one.
To Find the Characteristic
Case I. When the number is greater than 1.
The characteristic is one less than the number of digits in the left of decimal point in the given number.
e.g., 6.125 characteristic is O.
61.321 characteristic is 1.
725.132 characteristic is 2.
Case II. When the number is less than 1.
The characteristic is one more than the number of zero, between the decimal point and the fu-st significant digits of the number and it is negative.
e.g.. 0.7. characteristic is 1.
0.06712 characteristic ia 2.
0.00031 characteristic is 4.
Note In place of -1 or -2 etc.. we use 1 tone bar) and 2 (two bar) etc.
Properties of Logarithm
I. Characteristic of the logarithm of any number greater than I will be less than number of digits in the ‘integral part of the number’.
2. Characteristic of the logarithm of a number less than one negative and is one more than the number of zeros to the right of the decimal point in the number.
3. Since. a negative number can never be expressed as the power of 10, mantissa should always be kept positive. Hence, whenever characteristic ig negative, minus sign is placed above the characteristic and not to i. to show that the mantissa is always positive.
4. Mantissa of the logarithm of the number having same digits in the same order will be the same, irrespective of the position of the decimal point.
Anti-Logarithm
The positive number a is called the anti-logarithm of a number 6, if a Is anti-logarithm of b. then we write a = antilog b.
So, a = antilog b ⇔ log a = b
Important Results on Logarithm
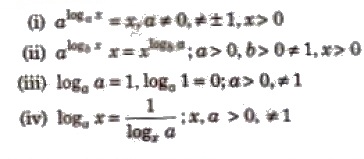

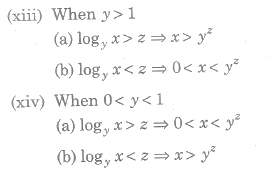
Logarithmic Inequalities
(i) Let a is a real number such that a > 0, ≠ 1, then
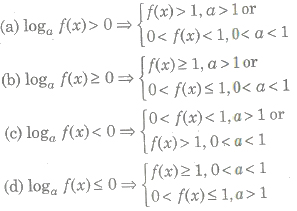
(ii) Let a is a real number, then

(iii) Let a is a real number such that a > 0, ≠ 1, then (a)
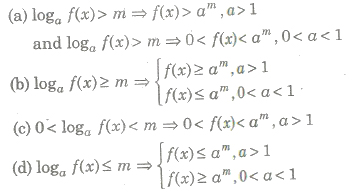
Class 11 Key Points, Important Questions & Practice Papers
Hope these notes helped you in your schools exam preparation. Candidates can also check out the Key Points, Important Questions & Practice Papers for various Subjects for Class 11 in both Hindi and English language form the link below.
Class 11 NCERT Solutions
Candidates who are studying in Class 11 can also check Class 11 NCERT Solutions from here. This will help the candidates to know the solutions for all subjects covered in Class 11th. Candidates can click on the subject wise link to get the same. Class 11 Chapter-wise, detailed solutions to the questions of the NCERT textbooks are provided with the objective of helping students compare their answers with the sample answers.
Class 11 Mock Test / Practice
Mock test are the practice test or you can say the blue print of the main exam. Before appearing in the main examination, candidates must try mock test as it helps the students learn from their mistakes. With the help of Class 11 Mock Test / Practice, candidates can also get an idea about the pattern and marking scheme of that examination. For the sake of the candidates we are providing Class 11 Mock Test / Practice links below.
Class 11 Exemplar Questions
Exemplar Questions Class 11 is a very important resource for students preparing for the Examination. Here we have provided Exemplar Problems Solutions along with NCERT Exemplar Problems Class 11. Question from very important topics is covered by Exemplar Questions for Class 11.
CBSE Notes for Class 11 Maths Biology Notes Physics Notes Chemistry Notes
To get study material, exam alerts and news, join our Whatsapp Channel.

