Class 11 Physics Gravitation – Get here the Notes for Class 11 Physics Gravitation. Candidates who are ambitious to qualify the Class 11 with good score can check this article for Notes. This is possible only when you have the best CBSE Class 11 Physics study material and a smart preparation plan. To assist you with that, we are here with notes. Hope these notes will helps you understand the important topics and remember the key points for exam point of view. Below we provided the Notes of Class 11 Physics for topic Gravitation.
- Class: 11th
- Subject: Physics
- Topic: Gravitation
- Resource: Notes
CBSE Notes Class 11 Physics Gravitation
Candidates who are pursuing in Class 11 are advised to revise the notes from this post. With the help of Notes, candidates can plan their Strategy for particular weaker section of the subject and study hard. So, go ahead and check the Important Notes for Class 11 Physics Gravitation from this article.
Every object in the universe attracts every other object with a force which is called the force of gravitation.
Gravitation is one of the four classes of interactions found in nature.
These are
(i) the gravitational force
(ii) the electromagnetic force
(iii) the strong nuclear force (also called the hadronic force).
(iv) the weak nuclear forces.
Although, of negligible importance in the interactions of elementary particles, gravity is of primary importance in the interactions of objects. It is gravity that holds the universe together.
Newton’s Law of Gravitation
Gravitational force is a attractive force between two masses m1 and m2 separated by a distance r.
The gravitational force acting between two point objects is proportional to the product of their masses and inversely proportional to the square of the distance between them.

Gravitational force.
where G is universal gravitational constant.
The value of G is 6.67 X 10-11 Nm2 kg-2 and is same throughout the universe.
The value of G is independent of the nature and size of the bodies well as the nature of the medium between them.
Dimensional formula of Gis [M-1L3T-2].
Important Points about Gravitation Force
(i) Gravitational force is a central as well as conservative force.
(ii) It is the weakest force in nature.
(iii) It is 1036 times smaller than electrostatic force and 10’l8times smaller than nuclear force.
(iv) The law of gravitational is applicable for all bodies, irrespective of their size, shape and position.
(v) Gravitational force acting between sun and planet provide it centripetal force for orbital motion.
(vi) Gravitational pull of the earth is called gravity.
(vii) Newton’s third law of motion holds good for the force of gravitation. It means the gravitation forces between two bodies are action-reaction pairs.
Following three points are important regarding the gravitational force
(i) Unlike the electrostatic force, it is independent of the medium between the particles.
(ii) It is conservative in nature.
(iii) It expresses the force between two point masses (of negligible volume). However, for external points of spherical bodies the whole mass can be assumed to be concentrated at its centre of mass.
Note Newton’s law of gravitation holde goods for object lying at uery large distances and also at very short distances. It fails when the distance between the objects is less than 10-9 m i.e., of the order of intermolecular distances.
Acceleration Due to Gravity
The uniform acceleration produced in a freely falling object due to the gravitational pull of the earth is known as acceleration due to gravity.
It is denoted by g and its unit is m/s2. It is a vector quantity and its direction is towards the centre of the earth.
The value of g is independent of the mass of the object which is falling freely under gravity.
The value of g changes slightly from place to place. The value of g is taken to be 9.8 m/s2 for all practical purposes.
The value of acceleration due to gravity on the moon is about. one sixth of that On the earth and on the sun is about 27 times of that on the earth.
Among the planets, the acceleration due to gravity is minimum on the mercury.
Relation between g and a is given by
g = Gm / R2
where M = mass of the earth = 6.0 * 1024 kg and R = radius of the earth = 6.38 * 106 m.
Acceleration due to gravity at a height h above the surface of the earth is given by
gh = Gm / (R+h)2 = g (1 – 2h / R)
Factors Affecting Acceleration Due to Gravity
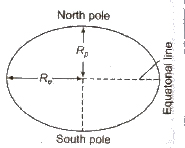
(i) Shape of Earth Acceleration due to gravity g &infi; 1 / R2 Earth is elliptical in shape. Its diameter at poles is approximately 42 km less than its diameter at equator.
Therefore, g is minimum at equator and maximum at poles.
(ii) Rotation of Earth about Its Own Axis If ω is the angular velocity of rotation of earth about its own axis, then acceleration due to gravity at a place having latitude λ is given by
g’ = g – Rω2 cos2 λ
At poles λ = 90° and g’ = g
Therefore, there is no effect of rotation of earth about its own axis at poles.
At equator λ = 0° and g’ = g – Rω2
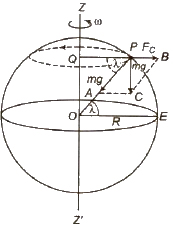
The value of g is minimum at equator
If earth stapes its rotation about its own axis, then g will remain unchanged at poles but increases by Rω2 at equator.
(iii) Effect of Altitude The value of g at height h from earth’s surface
g’ = g / (1 + h / R)2
Therefore g decreases with altitude.

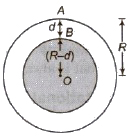
(iv) Effect of Depth The value of gat depth h A from earth’s surface
g’ = g * (1 – h / R)
Therefore g decreases with depth from earth’s surface.
The value of g becomes zero at earth’s centre.
Gravitational Field
The space in the surrounding of any body in which its gravitational pull can be experienced by other bodies is called gravitational field.
Intensity of Gravitational Field
The gravitational force acting per unit mass at Earth any point in gravitational field is called intensity of gravitational field at that point.
It is denoted by Eg or I.
Eg or I = F / m

Intensity of gravitational field at a distance r from a body of mass M is given by
Eg or I = GM / r2
It is a vector quantity and its direction is towards the centre of gravity of the body.
Its S1 unit is N/m and its dimensional formula is [LT-2].
Gravitational mass Mg is defined by Newton’s law of gravitation.
Mg = Fg / g = W / g = Weight of body / Acceleration due to gravity
∴ (M1)g / (M2)g = Fg1g2 / Fg2g1
Gravitational Potential
Gravitational potential at any point in gravitational field is equal the work done per unit mass in bringing a very light body from infinity to that point.
It is denoted by Vg.
Gravitational potential, Vg = W / m = – GM / r
Its SI unit is J / kg and it is a scalar quantity. Its dimensional formula is [L3r-2].
Since work W is obtained, that is, it is negative, the gravitational potential is always negative.
Gravitational Potential Energy
Gravitational potential energy of any object at any point in gravitational field is equal to the work done in bringing it from infinity to that point. It is denoted by U.
Gravitational potential energy U = – GMm / r
The negative sign shows that the gravitational potential energy decreases with increase in distance.
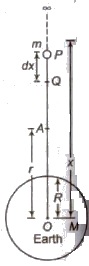
Gravitational potential energy at height h from surface of earth
Uh = – GMm / R + h = mgR / 1 + h/R
Satellite
A heavenly object which revolves around a planet is called a satellite. Natural satellites are those heavenly objects which are not man made and revolve around the earth. Artificial satellites are those neaven objects which are man made and launched for some purposes revolve around the earth.
Time period of satellite
T = 2π √r3 / GM
= 2π √(R + h)3 / g [ g = GM / R2
Near the earth surface, time period of the satellite
T = 2π √R3 / GM = √3π / Gp
T = 2π √R / g = 5.08 * 103 s = 84 min.
where p is the average density of earth.
Artificial satellites are of two types :
1. Geostationary or Parking Satellites
A satellite which appears to be at a fixed position at a definite height to an observer on earth is called geostationary or parking satellite.
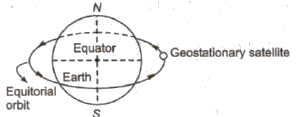
Height from earth’s surface = 36000 km
Radius of orbit = 42400 km
Time period = 24 h
Orbital velocity = 3.1 km/s
Angular velocity = 2π / 24 = π / 12 rad / h
There satellites revolve around the earth in equatorial orbits.
The angular velocity of the satellite is same in magnitude and direction as that of angular velocity of the earth about its own axis.
These satellites are used in communication purpose.
INSAT 2B and INSAT 2C are geostationary satellites of India.
2. Polar Satellites
These are those satellites which revolve in polar orbits around earth. A polar orbit is that orbit whose angle of inclination with equatorial plane of earth is 90°.
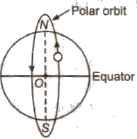
Height from earth’s surface = 880 km
Time period = 84 min
Orbital velocity = 8 km / s
Angular velocity = 2π / 84 = π / 42 rad / min.
There satellites revolve around the earth in polar orbits.
These satellites are used in forecasting weather, studying the upper region of the atmosphere, in mapping, etc.
PSLV series satellites are polar satellites of India.
Orbital Velocity
Orbital velocity of a satellite is the minimum velocity required to the satellite into a given orbit around earth.
Orbital velocity of a satellite is given by
vo = √GM / r = R √g / R + h
where, M = mass of the planet, R = radius of the planet and h = height of the satellite from planet’s surface.
If satellite is revolving near the earth’s surface, then r = (R + h) =- R
Now orbital velocity,
vo = √gR
= 7.92km / h
if v is the speed of a satellite in its orbit and vo is the required orbital velocity to move in the orbit, then
(i) If v < vo, then satellite will move on a parabolic path and satellite falls back to earth.
(ii) If V = vo then satellite revolves in circular path/orbit around earth.
(iii) If vo < V < ve then satellite shall revolve around earth in elliptical orbit.
Energy of a Satellite in Orbit
Total energy of a satellite
E = KE + PE
= GMm / 2r + (- GMm / r)
= – GMm / 2r
Binding Energy
The energy required to remove a satellite from its orbit around the earth (planet) to infinity is called binding energy of the satellite.
Binding energy of the satellite of mass m is given by
BE = + GMm / 2r
Escape Velocity
Escape velocity on earth is the minimum velocity with which a body has to be projected vertically upwards from the earth’s surface so that it just crosses the earth’s gravitational field and never returns.
Escape velocity of any object
ve = √2GM / R
= √2gR = √8πp GR2 / 3
Escape velocity does not depend upon the mass or shape or size of the body as well as the direction of projection of the body.
Escape velocity at earth is 11.2 km / s.
Some Important Escape Velocities
| Heavenly body | Escape velocity |
| Moon | 2.3 km/s |
| Mercury | 4.28 km/s |
| Earth | 11.2 km/s |
| Jupiter | 60 km/s |
| Sun | 618 km/s |
| Neutron star | 2 x 105 km/s |
Relation between escape velocity and orbital velocity of the satellite
ve = √2 vo
If velocity of projection U is equal the escape velocity (v = ve), then the satellite will escape away following a parabolic path.
If velocity of projection u of satellite is greater than the escape velocity ( v > ve), then the satellite will escape away following a hyperbolic path.
Weightlessness
It is a situation in which the effective weight of the body becomes zero,
Weightlessness is achieved
(i) during freely falling under gravity
(ii) inside a space craft or satellite
(iii) at the centre of the earth
(iv) when a body is lying in a freely falling lift.
Kepler’s Laws of Planetary Motion
(i) Law of orbit Every planet revolve around the sun in elliptical orbit and sun is at its one focus.

(ii) Law of area The radius vector drawn from the sun to a planet sweeps out equal areas in equal intervals of time, i.e., the areal velocity of the planet around the sun is constant.
Areal velocity of a planet
dA / dt = L / 2m = constant
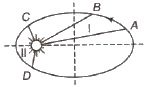
where L = angular momentum and m = mass of the planet.
(iii) Law of period The square of the time period of revolution of planet around the sun is directly proportional to the cube semi-major axis of its elliptical orbit.
T2 &infi; a3 or (T1 / T2)2 = (a1 / a2)3
where, a = semi-major axis of the elliptical orbit.
Important Points
(i) A missile is launched with a velocity less than the escape velocity. The sum of its kinetic energy and potential energy is negative.
(ii) The orbital speed of jupiter is less than the orbital speed of earth.
(iii) A bomb explodes on the moon. You cannot hear the sound of the explosion on earth.
(iv) A bottle filled with water at 30°C and fitted with a cork is taken to the moon. If the cork is opened at the surface of the moon then water will boil.
(v) For a satellite orbiting near earth’s surface
(a) Orbital velocity = 8 km / s
(b) Time period = 84 min approximately
(c) Angular speed ω = 2π / 84 rad / min
= 0.00125 rad / s
(vi) Inertial mass and gravitational mass
(a) Inertial mass = force / acceleration
(b) Gravitational mass = weight of body / acceleration due to gravity
(c) They are equal to each other in magnitude.
(d) Gravitational mass of a body is affected by the presence of other bodies near it. Inertial mass of a body remains unaffected by the presence of other bodies near it.
Class 11 Key Points, Important Questions & Practice Papers
Hope these notes helped you in your schools exam preparation. Candidates can also check out the Key Points, Important Questions & Practice Papers for various Subjects for Class 11 in both Hindi and English language form the link below.
Class 11 NCERT Solutions
Candidates who are studying in Class 11 can also check Class 11 NCERT Solutions from here. This will help the candidates to know the solutions for all subjects covered in Class 11th. Candidates can click on the subject wise link to get the same. Class 11 Chapter-wise, detailed solutions to the questions of the NCERT textbooks are provided with the objective of helping students compare their answers with the sample answers.
Class 11 Mock Test / Practice
Mock test are the practice test or you can say the blue print of the main exam. Before appearing in the main examination, candidates must try mock test as it helps the students learn from their mistakes. With the help of Class 11 Mock Test / Practice, candidates can also get an idea about the pattern and marking scheme of that examination. For the sake of the candidates we are providing Class 11 Mock Test / Practice links below.
Class 11 Exemplar Questions
Exemplar Questions Class 11 is a very important resource for students preparing for the Examination. Here we have provided Exemplar Problems Solutions along with NCERT Exemplar Problems Class 11. Question from very important topics is covered by Exemplar Questions for Class 11.
CBSE Notes for Class 11 Physics Notes Biology Notes Maths Notes Chemistry Notes
To get study material, exam alerts and news, join our Whatsapp Channel.

