CBSE Class 11 Maths Sequences and Series – Get here the Notes for Class 11 Sequences and Series. Candidates who are ambitious to qualify the Class 11 with good score can check this article for Notes. This is possible only when you have the best CBSE Class 11 Maths study material and a smart preparation plan. To assist you with that, we are here with notes. Hope these notes will helps you understand the important topics and remember the key points for exam point of view. Below we provided the Notes of CBSE Class 11 Maths for topic Sequences and Series.
- Class: 11th
- Subject: Maths
- Topic: Sequences and Series
- Resource: Notes
CBSE Notes Class 11 Maths Sequences and Series
Candidates who are pursuing in CBSE Class 11 Maths are advised to revise the notes from this post. With the help of Notes, candidates can plan their Strategy for particular weaker section of the subject and study hard. So, go ahead and check the Important Notes for CBSE Class 11 Maths Sequences and Series from this article.
1. Sequence: Sequence is a function whose domain is a subset of natural numbers. It represents the images of 1, 2, 3,… ,n, as f1, f2, f3, …., fn , where fn = f(n).
2. Real Sequence: A sequence whose range is a subset of R is called a real sequence.
3. Series: If a1, a2, a3 , … , an is a sequence, then the expression a1 + a2 + a3 + … + an is a series.
4. Progression: A sequence whose terms follow certain rule is called a progression.
5. Finite Series: A series having finite number of terms is called finite series.
6. Infinite Series: A series having infinite number of terms is called infinite series.
Arithmetic Progression (AP)
A sequence in which the difference of two consecutive terms is constant, is called Arithmetic Progression (AP).
Properties of Arithmetic Progression
(i) If a sequence is an AP, then its nth term is a linear expression in n, i.e., its nth term is given by An + B, where A and B are constants and A = common difference.
(ii) nth Term of an AP If a is the first term, d is the common difference and / is the last term of an AP, then
(a) nth term is given by 1= an = a + (n – 1)d
(b) nth term of an AP from the last term is a’n = l – (n – 1)d
(c) an + a’n = a + 1
i.e., nth term from the start + nth term from the end
= constant
= first term + last term
(d) Common difference of an AP
d = Tn – Tn-1, ∀ n > 1
(e) Tn = 1/2[Tn-k + Tn+k], k < n
(iii) If a constant is added or subtracted from each term of an AP, then the resulting sequence is an AP with same common difference.
(iv) If each term of an AP is multiplied or divided by a non-zero constant k, then the resulting sequence is also an AP, with common difference kd or d/k where d = common difference.
(v) If an, an+1 and an+2 are three consecutive terms of an AP, then 2an+1 = an + an+2.
(vi) (a) Any three terms of an AP can be taken as a – d, a, a + d.
(b) Any four terms of an AP can be taken as a-3d,a- d, a + d, a + 3d.
(c) Any five terms of an AP can be taken as a-2d,a – d, a, a + d, a + 2d.
(vii) Sum of n Terms of an AP
(a) Sum of n terms of AP, is given by Sn = n/2[2a + (n – 1)d] = n/2[a + l]
(b) A sequence is an AP, iff the sum of n terms is of the form An2 + Bn, where A and B are constants. Common difference in such case will be 2A.
(c) Tn = Sn – Sn-1
(viii) a2, b2 and c2 are in AP.

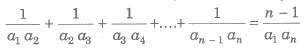
(ix) If a1, a2,…, an are the non-zero terms of an AP, then
(x) Arithmetic Mean
(a) If a, A and b are in AP, then A= (a + b)/2 is called the 2 arithmetic mean of a and b.
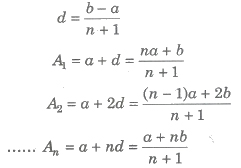
(b) If a1, a2, a3 , an are n numbers, then their AM is given by,
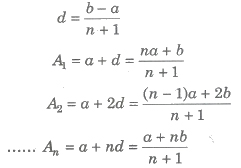
(c) If a, A1 , A2 , A3 ,…,An, b are in AP, then A1, A2, A3,…, An are n arithmetic mean between a and b, where

(d) Sum of n AM’s between a and b is nA
i.e., A1 + A2 + A3 + + = nA
Geometric Progression (GP)
A sequence in which the ratio of two consecutive terms is constant is called GP. The constant ratio is called common ratio (r).
i.e., an+1/an = r, ∀ n ≥ 1
Properties of Geometric Progression (GP)
(i) nth Term of a GP If a is the first term and r is the common ratio
(a) nth term of a GP from the beginning is an = arn-1
(b) nth term of a GP from the end is a’n = l/rn-1, l = last term
(c) If a is the first term and r is the common ratio of a GP, then the GP can be written as a, ar, ar2,… , arn-1, …
(d) The nth term from the end of a finite GP consisting of m terms is arm-n, where a is the first term and r is the common ratio of the GP.
(e) ana’n = al i.e., nth term from the beginning x nth term from the end = constant = first term x last term.
(ii) If all the terms of GP be multiplied or divided by same non-zero constant, then the resulting sequence is a GP with the same common ratio.
(iii) The reciprocal terms of a given GP form a GP.
(iv) If each term of a GP be raised to same power, the resulting sequence also forms a GP.
(v) If the terms of a GP are chosen at regular intervals, then the resulting sequence is also a GP.
(vi) If a1, a2, a3, … , an are non-zero, non-negative term of a GP, then
(a) GM = (a1a2a3… an )1/n
(b) log a1, log a2, log a3,…, log an are in an AP and vice-versa.
(vii) If a, b and c are three consecutive terms of a GP, then b2 = ac
(viii) (a) Three terms of a GP can be taken as a/r, a and ar.
(b) Four terms of a GP can be taken as a/r3, a/r, ar and ar3.
(c) Five terms of a GP can be taken as a/r2, a/r, ar and ar2.
(ix) Sum of n Terms of a GP

(a) Sum of n terms of a GP is given by
(x) Geometric Mean (GM)
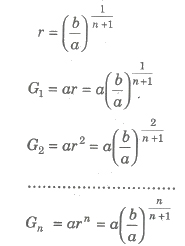
(a) If a, G, b are in GP, then G is called the geometric mean of a and b and is given by G = √ab
(b) If a, G1, G2, G3, , Gn, b are in GP, then G1, G2, G3,… , Gn, are in GM’s between a and b, where

(c) Product of n GM’s, G1 X G2 X G3 X … X Gn = Gn
Harmonic Progression (HP)
A sequence a1, a2, a3 ,…, an of non-zero numbers is called a Harmonic Progression (HP), if the sequence 1/a1, 1/a2, 1/a3, …, 1/an is an AP.
Properties of Harmonic Progression (HP)
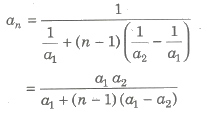
(i) nth term of HP, if a1, a2, a3 ,…, an are in HP, then
(a) nth term of the HP from the beginning
(b) nth term of the HP from the end
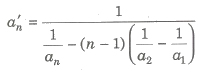

(d) an = 1/a+(n-1)d are the first term and common difference of the corresponding AP.
(ii) Sum of harmonic progression does not exist.
Harmonic Mean
(i) If a, H,b are in HP, then H is called the harmonic mean of a and b i.e., H= 2ab/(a + b)
(ii) If a, H1, H2, H3, …, Hn, b are in HP, then
H1, H2, H3, …, Hn
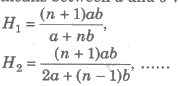
are n harmonic means between a and b where

(iii) Harmonic Mean (HM) between a1, a2, a3, …, an is given by
Properties of AM, GM and HM between Two Numbers
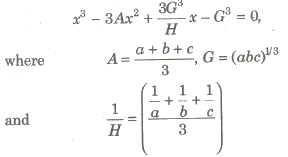
If A, G and H are arithmetic, geometric and harmonic means of two positive numbers a and b, then
(i) A=(a+b)/2, G=√ab, H=(2ab)/(a+b)
(ii) A≥G≥H
(iii) A, G, H are in GP and G2 = AH
(iv) If A,G,H are AM, GM and HM between three given numbers a, b and c, then the equation on having a, b and c as its root is
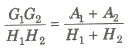
(v) If A1,A2 be two AM’s, G1, G2 be two GM’s and H1, H2 be two HM’s between two numbers a and b, then
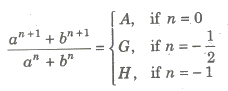
(vi) If A,G and H be AM, GM and HM between two numbers a and b, then
Arithmetico-Geometric Progression
A sequence in which every term is a product of a term of AP and GP is known as arithmetico-geometric progression.
The series may be written as

Sum of Arithmetico-Geometric Series

Type 1 Let al + a2 + a3 + … be a given series. If a2 – al, a3 – a2, … are in AP or GP, then an and Sn can be found by the method of difference.
where T1, T2, T3 ,… are terms of new series and Sn = Σan
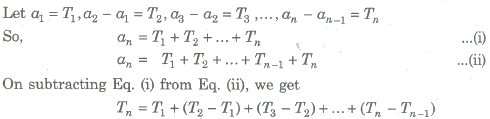
Type 2 It is not always necessary that the series of first order of differences i.e., a2 – a1, a3 – a2, …, an – an-1 is always either in AP or in GP in such case.
Now, the series (T2 — T1) + (T3 — T2) + …+ (Tn – Tn-1) is series of second order of differences and when it is either in AP or in GP, then an = a1 + ΣTr
Otherwise, in the similar way, we find series of higher order of differences and the nth term of the series.
Exponential Series
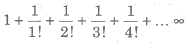
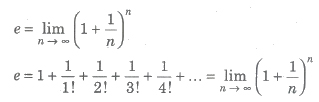
The sum of the series is denoted by the number e.
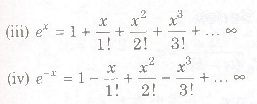
(i) e lies between 2 and 3.
(ii) e is an irrational number.
Exponential Theorem
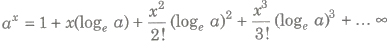

Let a>0, then for all real value of x,
Logarithmic Series

Important Result and Useful Series
24. If number of terms in AP/GP/HP are odd, then AM/GM/HM of first and last term in middle term of progression.
25. If pth, qth and rth term of geometric progression are also in geometric progression.
26. If a,b and c are in AP and also in GP, then a=b=c
27. If a, b and c are in AP, then xa, xb and xc are in geometric progression.
Class 11 Key Points, Important Questions & Practice Papers
Hope these notes helped you in your schools exam preparation. Candidates can also check out the Key Points, Important Questions & Practice Papers for various Subjects for Class 11 in both Hindi and English language form the link below.
Class 11 NCERT Solutions
Candidates who are studying in Class 11 can also check Class 11 NCERT Solutions from here. This will help the candidates to know the solutions for all subjects covered in Class 11th. Candidates can click on the subject wise link to get the same. Class 11 Chapter-wise, detailed solutions to the questions of the NCERT textbooks are provided with the objective of helping students compare their answers with the sample answers.
Class 11 Mock Test / Practice
Mock test are the practice test or you can say the blue print of the main exam. Before appearing in the main examination, candidates must try mock test as it helps the students learn from their mistakes. With the help of Class 11 Mock Test / Practice, candidates can also get an idea about the pattern and marking scheme of that examination. For the sake of the candidates we are providing Class 11 Mock Test / Practice links below.
Class 11 Exemplar Questions
Exemplar Questions Class 11 is a very important resource for students preparing for the Examination. Here we have provided Exemplar Problems Solutions along with NCERT Exemplar Problems Class 11. Question from very important topics is covered by Exemplar Questions for Class 11.
CBSE Notes for Class 11 Maths Biology Notes Physics Notes Chemistry Notes
To get study material, exam alerts and news, join our Whatsapp Channel.

