Class 12 Maths Limits, Continuity and Differentiablity – Get here the Notes for Class 12 Maths Limits, Continuity and Differentiablity. Candidates who are ambitious to qualify the Class 12 with good score can check this article for Notes. This is possible only when you have the best CBSE Class 12 Maths study material and a smart preparation plan. To assist you with that, we are here with notes. Hope these notes will helps you understand the important topics and remember the key points for exam point of view. Below we provided the Notes of Class 12 Maths for topic Limits, Continuity and Differentiablity.
- Class: 12th
- Subject: Maths
- Topic: Limits, Continuity and Differentiablity
- Resource: Notes
CBSE Notes Class 12 Maths Limits, Continuity and Differentiablity
Candidates who are pursuing in Class 12 are advised to revise the notes from this post. With the help of Notes, candidates can plan their Strategy for particular weaker section of the subject and study hard. So, go ahead and check the Important Notes for Class 12 Maths Limits, Continuity and Differentiablity
Limit
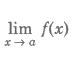
Let y = f(x) be a function of x. If at x = a, f(x) takes indeterminate form, then we consider the values of the function which is very near to a. If these values tend to a definite unique number as x tends to a, then the unique number, so obtained is called the limit of f(x) at x = a and we write it as .
Left Hand and Right Hand Limits
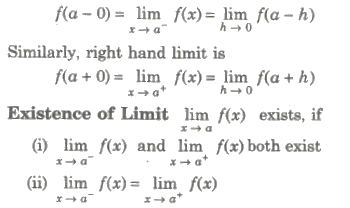
If values of the function at the points which are very near to a on the left tends to a definite unique number as x tends to a, then the unique number, so obtained is called the left hand limit of f(x) at x = a. We write it as
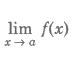
Uniqueness of Limit If exists, then it is unique. There cannot be two distinct numbers l1 and l2 such that when x tends to a, the function f(x) tends to both l1 and l2.
Fundamental Theorems on Limits

Important Results on Limit
1. Trigonometric Limits

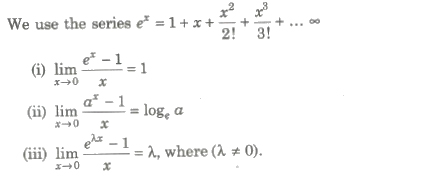
2. Exponential Limits
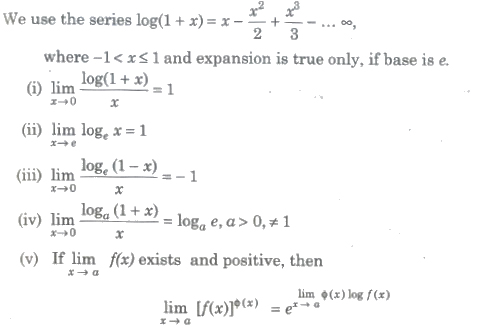
3. Logarithmic Limits

4. Based on the Form 1∞
Methods of Evaluating Limits


1. Determinate Forms (Limits by Direct Substitution)
To find we substitute x = a in the function. If the value x –> a comesout to be a definite value, it is the limit. That is = f(a) provided it exists.
2. Indeterminate Forms

If direct substitution of x = a while evaluating leads to one of the following form
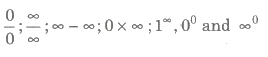
Then, it is called interminate form these limits can be counted by using L’ Hospitals’s rule or some other method given below.
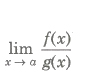
(i) Limits by Factorisation If attains 0/0 form, the x-a must be a factor of numerator and denominator which ca be cancelled out.
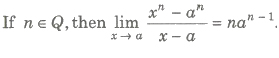

(ii) Limits by Substitution In order to evaluate a may substitute x = a + h or a – h, so that as x – a, h → 0. Thus


This method is applied to bring the limit at zero as the most formulae are given as .
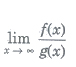
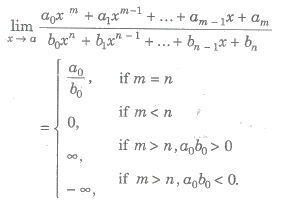
(iii) Limits of Functions as x → ∞
If is of the form ∞/∞ and f(x) and g(x) are both polynomial of x. Then, we divide numerator and denominator by the highest power of x and put 0 for -1/x.
If m and n are positive integers and a0, b0 # 0 are non-zero real numbers, then

L’Hospital’s Rule
Limit Using Expansions
Many limits can be ecaluated very easily by applying expansion series, some of the standard expansions are
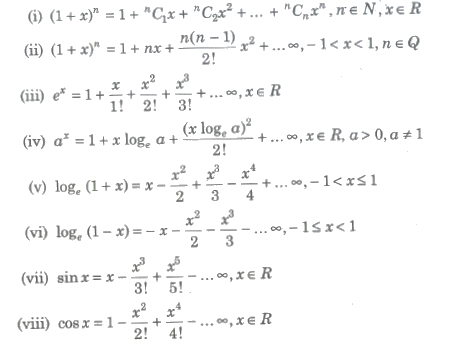
Important Result
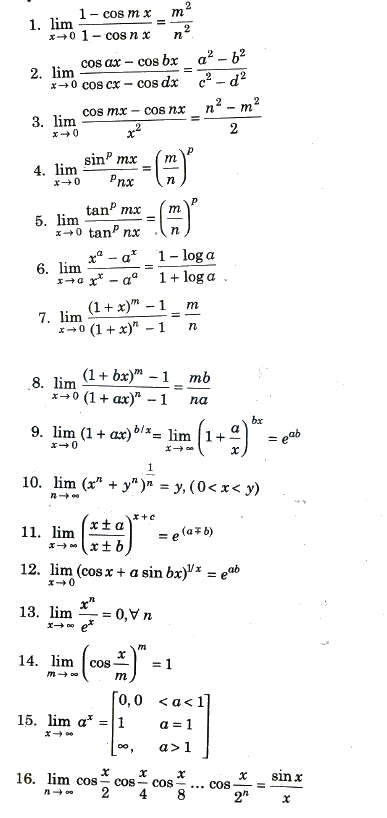
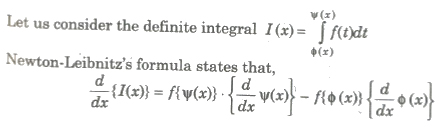
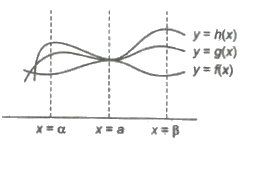
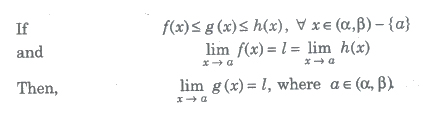
Use of newton-Leibnitz’s formula in Evaluating the Limits
Sandwich theorem
Continuity
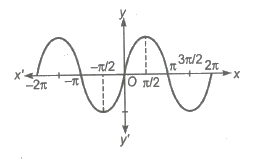

If the graph of a function has no break or gap, then it is continuous, otherwise it is discontinuous. A function which is not continuous is called a discontinuous function.
e.g., Graph of sin x is continuous
While f(x) = 1/x is discontinuous at x=0.
Continuity at a Point
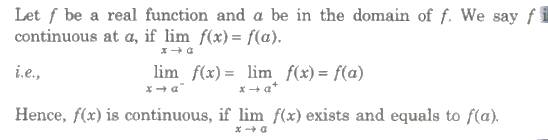
Cauchy’s Definition of Continuity
A function f is said to be continuous at a point a of its domain differentiate for every ε > 0 there exists ε > 0 (dependent on ε) such that |x-a| < δ ⇒ |f(x) – f(a)| < ε.
Heine’s Definition of Continuity
A function f is said to be continuous at a point ‘a’ of its domain D, if for every sequence < an > of the points in D converging to a, then the sequence < f(an) > converges to f(a) i.e., lim an = a = lim f (an) )= 1(a).
Discontinuity of a Function

The function f(x) can be discontinuous at a point x = a in any one of the following ways.
Important Points to be Remembered
(i) If f (x) is continuous and g(x) is discontinuous at x = a, then the product function φ(x) = f(x).g(x) is not necessarily be discontinuous at x = a.
(ii) If f (x) and g (x) both are discontinuous at x = a, then the product function φ(x) =f(x) g(x) is not necessarily be discontinuous at x = a.
Continuity of a Function in an Interval
(i) A function f(x) is said to be continuous in an open interval (a, b), if f(x) is continuous at every point of the interval.
(ii) A function f(x) is said to be continuous in a closed interval [a, b], if (x) is continuous in (a, b). In addition, f(x) is continuous at x = a from right limit and f(x) is continuous at x = b, from left limit.

Fundamental Theorems of Continuity
(i) If f and g are continuous functions, then
- f ± g and fg are continuous.
- cf is continuous, where c is a constant.
- f/g is continuous at those points, where g(x) ≠ 0.
(ii) If g is continuous at a point a and f is continuous at g(a), then fog is continuous at a.
(iii) If f is continuous in [a, b] , then it is bounded in [a, b] i.e. , there exist m and M such that
m ≤ f(x) ≤ M, ∀ x ∈ [a, b]
where m and M are called minimum and maximum values f(x) respectively in the interval [a, b].
(iv) If f is continuous in [a, b], then f assumes atleast once eve value between minimum and maximum values of f(x).
Thus, a ≤ x ≤ b ⇒ m ≤ f(x) ≤ M or range of f(x) = [m, M], x ε [a, b].
(v) If f is continuous in its domain, then |f| is also continuous in it domain.
(vi) If f is continuous at a and f (a) ≠ 0, then there exists an ope interval (a — δ, a + δ) such that for all x ε (a — δ, a + δ), f (x) has the same sing as f(a).
(vii) If f is a continuous function defined on [a, b] such that f (a) an f (b) are of opposite sign, then there exists atleast one solution the equation f(x)= 0 in the open interval (a, b).
(viii) If f is continuous on [a, b] and maps [a, b] into [a, b], then for some x ε [a , b], we have f (x)= x.
(ix) If f is continuous in domain D, then 1/f is also continuous in D – {x : f(x)= 0}.
(x) A function f(x) is said to be everywhere continuous, if it is continuous on the entire real line (-∞,∞)
Differentiability of a Function at a Point
The function f(x) is differentiable at a point P iff there exists a unique tangent at point P.
In other words, f(x) is differentiable at a point P iff the curve does not have P as a corner point i.e., the function is not differentiable at those points on which function has holes or sharp edges.

Let us consider the function f(x) = |x – 1|.
Differentiability in an Interval
A function f(x) is said to be differentiable in an interval (a, b), if f(x) is differentiable at every point of this interval (a, b).
A function f(x) is said to be differentiable in a closed interval [a, b], if f(x) is differentiable in (a, b), in addition f(x) is differentiable at x = a from right hand limit and differentiable at x = b from left hand limit.
Relation between Continuity and Differentiability
(i) If a function f(x) is differentiable at x = a, then f(x) is necessarily continuous at x = a but the converse is not necessary true.
(ii) The sum, difference, product and quotient of two differentiable function is differentiable. The composition of differentiable function is a differentiable funciton converse of (i) is not necessarily true i.e., if a function f(x) is continuous at x = a, then it is not necessarily differentiable at x = a e.g., f(x) =I xl is continuous at x = 0 but not differentiable at x = 0.
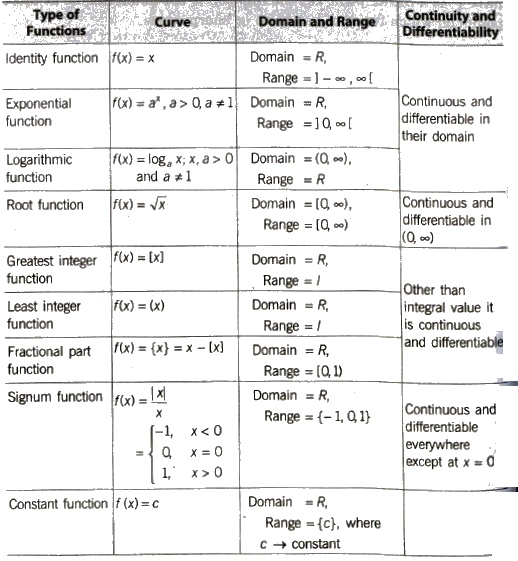
Continuity and Differentiability of Different Functions

Class 12 Key Points, Important Questions & Practice Papers
Hope these notes helped you in your schools exam preparation. Candidates can also check out the Key Points, Important Questions & Practice Papers for various Subjects for Class 12 in both Hindi and English language form the link below.
Class 12 NCERT Solutions
Candidates who are studying in Class 12 can also check Class 12 NCERT Solutions from here. This will help the candidates to know the solutions for all subjects covered in Class 12th. Candidates can click on the subject wise link to get the same. Class 12 Chapter-wise, detailed solutions to the questions of the NCERT textbooks are provided with the objective of helping students compare their answers with the sample answers.
Class 12 Mock Test / Practice
Mock test are the practice test or you can say the blue print of the main exam. Before appearing in the main examination, candidates must try mock test as it helps the students learn from their mistakes. With the help of Class 12 Mock Test / Practice, candidates can also get an idea about the pattern and marking scheme of that examination. For the sake of the candidates we are providing Class 12 Mock Test / Practice links below.
Class 12 Exemplar Questions
Exemplar Questions Class 12 is a very important resource for students preparing for the Examination. Here we have provided Exemplar Problems Solutions along with NCERT Exemplar Problems Class 12. Question from very important topics is covered by Exemplar Questions for Class 12.
Class 12 Maths
Chemistry Notes Physics Notes Biology Notes
To get study material, exam alerts and news, join our Whatsapp Channel.


