Candidates can download NCERT Exemplar Class 10 Maths Unit 1 from this page. The exemplar has been provided by the National Council of Educational Research & Training (NCERT) and the candidates can check it from below for free of cost. It contains objective, very short answer type, short answer type, and long answer type questions. Along with it, the answer for each question has also been provided. From the NCERT Exemplar Class 10 Maths Unit 1, candidates can understand the level and type of questions that are asked in the exam.
NCERT Exemplar Class 10 Maths Unit 1 Real Numbers
NCERT Class 10 Maths Unit 1 is for Real Numbers. The type of questions that will be asked from NCERT Class 10 Maths Unit 1 are displayed in the below provided NCERT Exemplar Class 10 Maths Unit 1. With the help of it, candidates can prepare well for the examination.
Also Check: NCERT Solutions for Class 10 Maths
Main Concepts and Results
Euclid’s Division Lemma : Given two positive integers a and b, there exist unique integers q and r satisfying a = bq + r, 0 ≤ r < b.
Euclid’s Division Algorithm to obtain the HCF of two positive integers, say c and d, c > d.
Step 1: Apply Euclid’s division lemma to c and d, to find whole numbers q and r, such that c = dq + r, 0 ≤ r < d.
Step 2: If r = 0, d is the HCF of c and d. If r ≠ 0, apply the division lemma to d and r.
Step 3 : Continue the process till the remainder is zero. The divisor at this stage will be the required HCF.
Fundamental Theorem of Arithmetic : Every composite number can be expressed as a product of primes, and this expression (factorisation) is unique, apart from the order in which the prime factors occur.
The sum or difference of a rational and an irrational number is irrational.
The product or quotient of a non-zero rational number and an irrational number is irrational.
For any two positive integers a and b, HCF (a, b) × LCM (a, b) = a × b.
Multiple Choice Questions (Solved Examples)
Choose the correct answer from the given four options:
Sample Question 1: The decimal expansion of the rational number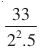 
will terminate after
(A) one decimal place (B) two decimal places (C) three decimal places (D) more than 3 decimal places
Solution: Answer (B)
Sample Question 2: Euclid’s division lemma states that for two positive integers a and b, there exist unique integers q and r such that a = bq + r, where r must satisfy
(A) 1 < r < b (B) 0 < r ≤ b (C) 0 ≤ r < b (D) 0 < r < b
Solution: Answer (C)
Multiple Choice Questions (Exercise)
Exercise- 1.1
Short Answer Questions with Reasoning (Solved Examples)
Sample Question 1: The values of the remainder r, when a positive integer a is divided by 3 are 0 and 1 only. Justify your answer.
Solution: No. According to Euclid’s division lemma, a = 3q + r, where 0 ≤ r < 3 and r is an integer.
Therefore, the values of r can be 0, 1 or 2.
Sample Question 2: Can the number 
, n being a natural number, end with the digit 5? Give reasons.
Solution: No, because 
, so the only primes in the factorisation of are 2 and 3, and not 5.
Hence, it cannot end with the digit 5.
Short Answer Questions with Reasoning (Exercise)
Exercise- 1.2
Short Answer Type Questions (Solved Examples)
Sample Question1: Using Euclid’s division algorithm, find which of the following pairs of numbers are co-prime:
(i) 231, 396 (ii) 847, 2160
Solution: Let us find the HCF of each pair of numbers.
(i) 396 = 231 × 1 + 165
231 = 165 × 1 + 66
165 = 66 × 2 + 33
66 = 33 × 2 + 0
Therefore, HCF = 33. Hence, numbers are not co-prime.
(ii) 2160 = 847 × 2 + 466
847 = 466 × 1 + 381
466 = 381 × 1 + 85
381 = 85 × 4 + 41
85 = 41 × 2 + 3
41 = 3 × 13 + 2
3 = 2 × 1 + 1
2 = 1 × 2 + 0
Therefore, the HCF = 1. Hence, the numbers are co-prime.
Sample Question 2: Show that the square of an odd positive integer is of the form 8m + 1, for some whole number m.
Solution: Any positive odd integer is of the form 2q + 1, where q is a whole number.
Sample Question 3: Prove that √2+√3 is irrational.
Solution: Let us suppose that √2+√3 is rational. Let √2+√3 = a , where a is rational.
Therefore,√2 = a − √3
Squaring on both sides, we get
2 = a² + 3 – 2a √3
Therefore, √3 = a²+1/2a, which is a contradiction as the right hand side is a rational number while √3 is irrational. Hence, √2+√3 is irrational.
Short Answer Type Questions (Exercise)
Exercise- 1.3
Long Answer Type Questions (Solved Examples)
Sample Question 1: Show that the square of an odd positive integer can be of the form 6q + 1 or 6q + 3 for some integer q.
Solution: We know that any positive integer can be of the form 6m, 6m + 1, 6m + 2, 6m + 3, 6m + 4 or 6m + 5, for some integer m.
Thus, an odd positive integer can be of the form 6m + 1, 6m + 3, or 6m + 5
Thus we have:
(6m+1)² = 36 m² + 12m + 1= 6 ( 6m² + 2m) + 1= 6q + 1, q is an integer
(6m+3)² = 36m² + 36m + 9 = 6 (6m²+6m + 1) + 3= 6q + 3, q is an integer
(6m + 5)² = 36m² + 60 m + 25 = 6 (6m²+ 10 m + 4) + 1 = 6q + 1, q is an integer.
Thus, the square of an odd positive integer can be of the form 6q + 1 or 6q + 3.
Long Answer Type Questions (Exercise)
Exercise 1.4
| Next » |
