Candidates can download NCERT Exemplar Class 11 Maths Unit 9 from this page. The exemplar has been provided by the National Council of Educational Research & Training (NCERT) and the candidates can check it from below for free of cost. It contains objective, very short answer type, short answer type, and long answer type questions. Along with it, the answer for each question has also been provided. From the NCERT Exemplar Class 11 Maths Unit 9, candidates can understand the level and type of questions that are asked in the exam.
NCERT Exemplar Class 11 Maths Unit 9 Sequence and Series
NCERT Exemplar Class 11 Maths Unit 9 is for Sequence and Series. The type of questions that will be asked from NCERT Class 11 Maths Unit 9 are displayed in the below provided NCERT Exemplar Class 11 Maths Unit 9. With the help of it, candidates can prepare well for the examination.
Also Check: NCERT Solutions for Class 11 Mathematics
Maths Important Questions Class 11 are given below.
9.1 Overview
By a sequence, we mean an arrangement of numbers in a definite order according to some rule. We denote the terms of a sequence by a1 , a2 , a3 , … , etc., the subscript denotes the position of the term. In view of the above a sequence in the set X can be regarded as a mapping or a function f : N → X defined by

Domain of f is a set of natural numbers or some subset of it denoting the position of term. If its range denoting the value of terms is a subset of R real numbers then it is called a real sequence.
A sequence is either finite or infinite depending upon the number of terms in a sequence.
We should not expect that its terms will be necessarily given by a specific formula.
However, we expect a theoretical scheme or rule for generating the terms.
Let a 1 , a 2 , a 3 , … , be the sequence, then, the expression a 1 + a 2 + a 3 + … is called the
series associated with given sequence. The series is finite or infinite according as the
given sequence is finite or infinite.
Remark When the series is used, it refers to the indicated sum not to the sum itself.
Sequence following certain patterns are more often called progressions. In
progressions, we note that each term except the first progresses in a definite manner.






9.1.1 Arithmetic progression (A.P.) is a sequence in which each term except the
first is obtained by adding a fixed number (positive or negative) to the preceding term.





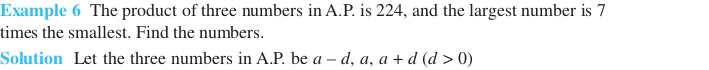

















9.2 Solved Examples
Short Answer Type
Long Answer Type
Objective Type Questions
Choose the correct answer out of the four given options in Examples 14 to 23 (M.C.Q.).
Short Type Questions

Long Type Questions

Objective Type Questions

Fill in the Blanks Type Questions
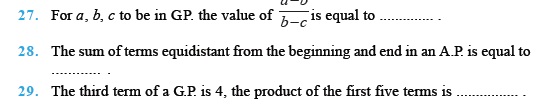
True or False Type Questions

Match Type Questions

Click here to download the NCERT Exemplar Class 11 Maths Unit 9 Sequence and Series.
Answers to Objective Type Questions

To get study material, exam alerts and news, join our Whatsapp Channel.

