CBSE Class 11 Chemistry Atomic Structure– Get here the Notes for CBSE Class 11 Chemistry Atomic Structure. Candidates who are ambitious to qualify the CBSE Class 11 Chemistry with good score can check this article for Notes. This is possible only when you have the best CBSE Class 11 Chemistry study material and a smart preparation plan. To assist you with that, we are here with notes. Hope these notes will helps you understand the important topics and remember the key points for exam point of view. Below we provided the Notes of Class 11 Chemistry for topic Atomic Structure.
- Class: 11th
- Subject: Chemistry
- Topic: Atomic Structure
- Resource: Notes
CBSE Class 11 Chemistry Notes : Atomic Structure
Candidates who are pursuing in CBSE Class 11 CHemistry are advised to revise the notes from this post. With the help of Notes, candidates can plan their Strategy for particular weaker section of the subject and study hard. So, go ahead and check the Important Notes for CBSE Class 11 Chemistry Atomic Structure from this article.
Atom
John Dalton proposed (in 1808) that atom is the smallest indivisible particle of matter. Atomic radii are of the order of 10-8cm. It contain three subatomic particles namely electrons, protons and neutrons,
Electron
Electron was discovered as a result of study of cathode rays by JJ Thomson. It was named by Stony
It carries a unit negative charge (-1.6 * 10-19 C).
Mass of electron is 9.11 * 10-31 kg and mass of one mole of electron is 0.55 mg.
Some of the characteristics of cathode rays are:
- These travel in straight line away from cathode and produce fluorescence when strike the glass wall of discharge tube.
- These cause mechanical motion in a small pin wheel placed – their path.
- These produce X-rays when strike with metal and are deflected by electric and magnetic field
Proton
Rutherford discovered proton on the basis of anode ray experiment.
It carries a unit positive charge (+1.6 * 10-19) C).
The mass of proton is 1.007276 U.
The e / m ratio of proton is 9.58 * 10-4 C / g. (e / m ratio is maximum for hydrogen gas.)
Some of the characteristics of anode rays are :
- These travel in straight line and posses mass many times the mass of an electron.
- These are not originated from anode.
- These also cause mechanical motion and are deflected by electric and magnetic field.
- Specific charge (e / m) for these rays depends upon the nature of the gas taken and is maximum for H2
Neutron
Neutrons are neutral particles. It was discovered by Chadwick (1932). The mass of neutron is 1.675x 10-24 g or 1.008665 amu or u.
94Be + 42He → 126C + 10n
Some Uncommon Subatomic Particles
(a) Positron Positive electron (0+1e), discovered by Dirac (1930) and Anderson (1932).
(b) Neutrino and antineutrino Particles of small mass and no charge as stated by Fermi (1934).
(c) Meson Discovered by Yukawa (1935) and Kemmer. They are unstable particles and include pi ions [pi;+, pi;– or pi;0].
(d) Anti-proton It is negative proton produced by Segre and Weigand (1955).
Thomson’s Atomic Model
Atom is a positive sphere with a number of electrons distributed within the sphere. It is also known as plum pudding model. It explains the neutrality of an atom. This model could not explain the results of Rutherford scattering experiment.
Rutherford’s Nuclear Model of Atom
It is based upon a-particle scattering experiment. Rutherford presented that
- Most part of the atom is empty.
- Atom possesses a highly dense, positively charged centre, called nucleus of the order 10-13cm.
- Entire mass of the atom is concentrated inside the nucleus.
- Electrons revolve around the nucleus in circular orbits.
- Electrons and the nucleus are held together by electrostatic forces of attraction.
Drawbacks of Rutherford’s Model
1. According to electromagnetic theory, when charged particles accelerated, they emit electromagnetic radiations, which CODIlE by electronic motion and thus orbit continue to shrink, so atom unstable. It doesn’t explain the stability of atom.
2. It doesn’t say anything about the electronic distribution electrons around nucleus.
Atomic Number
Atomic number of an element corresponds to the total number protons present in the nucleus or total number of electrons present the neutral atom
Mass Number
Mass number of an element
= number of protons + number of neutrons

Electromagnetic Wave Theory (Maxwell)
The energy is emitted from source continuously in the form of radiations and magnetic fields. All electromagnetic waves travel with the velocity of light (3 * 108 m / s) and do not require any medium for their propagation.
An electromagnetic wave has the following characteristics:
(i) Wavelength It is the distance between two successive crests or troughs of a wave. It is denoted by the Greek letter λ (lambda).
(ii) Frequency It represents the number of waves which pass through a given point in one second. It is denoted by v (nu).
(iii) Velocity (v) It is defined as the distance covered in one second by the waves. Velocity of light is 3 * 1010 cms-1
(iv) Wave number It is the reciprocal of wavelength and has units cm-1 It is denoted by v (nu bar).
(v) Amplitude (a) It is the height of the crest or depth of the trough of a wave.
Wavelength (λ), frequency (v) and velocity (c) of any electromagnetic radiations are related to each other as c = vλ
Electromagnetic Spectrum
The different types of electromagnetic radiations differ only in their wavelengths and hence. frequencies. When these electromagnetic radiations are arranged in order to their increasing wavelengths or decreasing frequencies, the complete spectrum obtained is called electromagnetic spectrum.
Different Types of Radiations and Their Sources

Electromagnetic spectra may be emission or absorption spectrum on the basis of energy absorbed or emitted. An emission spectrum is obtained when a substance emits radiation after absorbing energy. An absorption spectra is obtained when a substance absorbs certain wavelengths and leave dark spaces in bright continuous spectrum.
Electromagnetic wave theory was successful in explaining the properties of light such as interference. diffraction etc., but it could not explain the following
1. Black body radiation
2. Photoelectric effect
These phenomena could be explained only if electromagnetic waves are supposed to have particle nature.
1. Black Body Radiation
If the substance being heated is a black body. the radiation emitted is called black body radiation.
2. Photoelectric Effect
It is the phenomenon in which beam of light of certain frequency falls on the surface of metal and electrons are ejected from it.
This phenomenon is known as photoelectric effect. It was first observed by Hertz.
Wo< = hvo
Wo< = hc / λmax
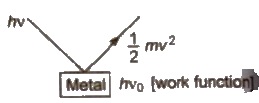
Threshold frequency (vo) = minimum frequency of the radiation
Work function (Wo) = required minimum energy of the radiation
E = KE + Wo
∴ 1 / 2 mv2 = h(v – vo)
[Kinetic energy of ejected electron = h(v – vo)
where; v = frequency of incident radiation
vo = threshold frequency
Particle Nature of Electromagnetic Radiation :
Planck’s Quantum Theory
Planck explain the distribution of intensity of the radiation from black body as a function of frequency or wavelength at different temperatures.
E = hv = hc / λ
where, h = Planck’s constant = 6.63 x 10-34 j-s
E = energy of photon or quantum
v = frequency of emitted radiation
If n is the number of quanta of a particular frequency and ET be total energy then Et = nhv
Bohr’s Model
Neils Bohr proposed his model in 1931. Bohr’s model is applicable only for one electron system like H, He+, Li2+ etc.
Assumptions of Bohr’s model are
1. Electrons keep revolving around the nucleus in certain fixed permissible orbits where it doesn’t gain or lose energy. These orbits are known as stationary orbits.
Number of waves in an orbit = circumstances of orbit / wavelength
2. The electrons can move only in those orbits for which the angular momentum is an integral multiple of h / 2π, i.e.,
mvr = nh / 2π
where, m = mass of electron: v = velocity of electron;
r = radius of orbit
n = number of orbit in which electrons are present
3. Energy is emitted or absorbed only when an electron Jumps from higher energy level to lower energy level and vice-versa.
ΔE = E2 – E1 = hv = hc / λ
4. The most stable state of an atom is its ground state or normal state,
From Bohr’s model, energy, velocity and radius of an electron in nth Bohr orbit are
(i) Velocity of an electron in nth Bohr orbit
(vn) = 2.165 * 106 Z / n m / s
(ii) Radius of nth Bohr orbit
(rn) = 0.53 * 10-10 n2 / Z m = 0.53 n2 / Z A
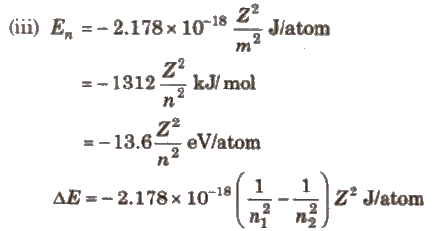
where, 11 = number of shell; Z = atomic number
As we go away from the nucleus, the energy levels come closer, i.e., with the increase in the value of n, the difference of energy between successive orbits decreases.
Thus. E2 – E1 > E3 – E2 > E4 – E3 > E5 – E4etc.
Sommerfeld Extension to Bohr’s Model
According to this theory. the angular momentum of revolving electron in all elliptical orbit is an integral multiple of h / 2π, i.e.,
mur = kh / 2π
From Bohr model, mur = nh / 2π
For K shell. n = 1,k = 1 Circular shape
L shell. n ; 2. k = 1. 2 Circular
M shell, n = 3. k = 1.2.3 Elliptical
N shell. n = 4, k =1 . 2, 3. 4 Elliptical
Emission Spectrum of Hydrogen
According to Bohr’s theory. when an electron jumps from ground states to excited state. it emits a radiation of definite frequency (or wavelength). Corresponding to the wavelength of each photon of light emitted, a bright line appears in the spectrum.
The number of spectral lines in the spectrum when the electron comes from nth level to the ground level = n(n – 1) / 2
Hydrogen spectrum consist of line spectrum.
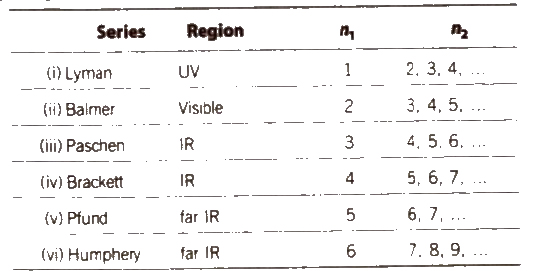
Wave number v is defined as reciprocal of the wavelength.
v = 1 / λ
v = RZ2 (1 / n21 – n22)
Here, λ = wavelength
R = Rydberg constant = 109677.8 cm-1
First line of a series is called line of longest wavelength (shortest energy) and last line of a series is the line of shortest wavelength highest energy, n2 = φ).
Limitations of Bohr’s Theory
1. It is unable to explain the spectrum of atom other than hydrogen like doublets or multielectron atoms.
2. It could not explain the ability of atom to form molecules by chemical bonds. Hence. it could not predict the shape of molecules.
3. It is not in accordance with the Heisenberg uncertainty principle and could not explain the concept of dual character of matter.
4. It is unable to explain the splitting of spectral lines in the presence of magnetic field (Zeeman effect) and electric field (Stark effect)
de-Broglie Principle
de-Broglie explains the dual nature of electron i.e.. both particle as well as wave nature.
λ = h / mv
where, λ = wavelength: v = velocity of particle; m = mass of particle
λ = h / √2m * K E
where, KE = kinetic energy.
Heisenberg’s Uncertainty Principle
According this principle, “it is impossible to specify at any give instant both the momentum and the position of subatomic particles like electron.”
Δx . ΔP ≥ h / 4π
where, Δx = uncertainty in position; Δp = uncertainty in momentum
Quantum Mechanical Model of Atom
It is the branch of chemistry which deals with dual behaviour of matter. It IS given by Werner Heisenberg and Erwin Schrodinger
Schrodinger wave equation is
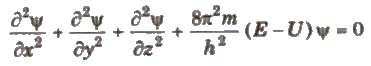
where. x, y, z = cartesian coordinates
m = mass of electron, E = total energy of electron
U =potential energy of electron, h =Planck’s constant
Ψ (Psi) = wave function which gives the amplitude of wave
Ψ2 = probability function
For H-atom. the equation is solved as
HΨ = EΨ
where, H is the total energy operator, called Hamiltonian. If the sum of kinetic energy operator (T) and potential energy operator (U) is the total energy. E of the system,
H = T + U
(T + U)Ψ = EΨ
[The atomic orbitals can be represented by the product of two wave functions (i) radial wave function (ii) angular wave function.
The orbital wave function, Ψ has no significance, but Ψ2 has significance, it measures the electron probability density at a point In an atom. Ψ can he positive or negative but ‘I’:? is always positive.
Probability Diagrams
The graph plotted between Ψ2 and distance from nucleus is called probability diagrams.

Node
A region or space, where probability of finding an electron is maximum is called a peak, while zero probability space is called node. Nodes are of two types:
(a) Radial nodes
(b) Angular nodes
(i) (n – I – 1) = radial node
(ii) (l) = angular node
(iii) (n – 1) = total + node
Number of Peaks and Nodes for Various Orbitals
| S. No. | Type of orbital | Number of peaks | |
| 1 | s | n | n – 1 |
| 2 | p | n – 1 | n – 2 |
| 3 | d | n – 2 | n – 3 |
| 4 | f | n – 3 | n – 4 |
Quantum Numbers
Each electron in an atom is identified in terms of four quantum numbers.
Principal Quantum Number (Niels Bohr)
It is denoted by 11. It tells us about the main shell in which electron resides. It also gives an idea about the energy of shell and average distance of the electron from the nucleus. Value of n = any integer.
Azimuthal Quantum Number (Sommerfeld)
It is denoted by I. It tells about the number of subshells (s. p, d, f) in any main shell. It also represent the angular momentum of an electron and shapes of subshells. The orbital angular momentum of an
electron = √l (l + 1) h / 2π
Value of l = 0 to n – 1.
I = 0 for s, I = 2 for d
I = 1 for P. / = 3 for f
Number of subshells in main energy level = n.
Magnetic Quantum Number (Lande)
is denoted by m. It tells about the number of orbitals and orientation of each subshell. Value of m = – l to + 1 including zero.
Number of orbitals in each subshell = ( 2l + 1)
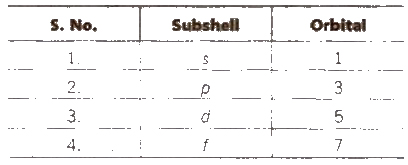
Number of orbitals in main energy level = n2
Spin Quantum Number (Uhlenbeck and Goldsmith)
“It is denoted by m, or s. It indicates the direction of spinning of electron, i.e., clockwise or anti- clockwise.
Maximum number of electrons in main energy level = 2n2
Difference between Orbit and Orbital

Electronic Configuration
Arrangement of electrons in the space around nucleus in an atom known as electronic configuration
Pauli Exclusion Principle
It states, no two electrons in an atom can have identical set of four quantum numbers.
The maximum number of electrons in s subshell is 2, p subshell is 6 d subshell is 10 and f subshell is 14.
Aufbau Principle
According to this principle, in the ground state of an atom, the electrons occupy the lowest energy orbitals available to them, i.e., the orbitals are filled in order of increasing value of n + l. For the orbitals having the same value of n + 1, the orbital having lower value of n is filled up first.
The general order of increasing energies of the orbital is
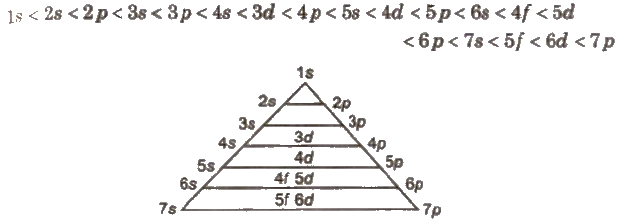
The energy of atomic orbitals for H-atom varies as
Is < 2s = 2P < 3s 3p = 3d < 4s = 4P = 4d = 4f
Half-filled and completely filled electronic configurations are more stable Hence. outer configuration of Cr is 3d5 4s1 and Cu is 3d10 4s1.
Hund’s Rule of Maximum Multiplicity
It states.
(i) In an atom no electron pairing takes place in the p, d or ( orbital. until each orbital of the given subshell contains one electron.
(ii) The unpaired electrons present in the various orbitals of the same subshell should have parallel spins.
Methods of Writing Electronic Configuration
(i) Orbital method In this, the electrons present in respective orbitals are denoted. e.g CI(17) = 1s2, 2s2, 2 p6, 3 2, 3 p5.
(ii) Shell method In this, the number of electrons in each shell is continuously written. e.g., Cl (17) =
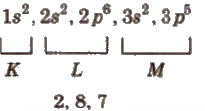
(iii) Box.method In this method, each orbital is denoted by a box and electrons are represented by half-headed (↑) or full-headed (↑) arrows. An orbital can occupy a maximum of two electrons.
e.g.,

Electronic Configuration of Ions
To write the electronic configuration of ions. first write the electronic configuration of neutral atom and then add (for negative charge) or remove (for positive charge) electrons in outer shell according to the nature and magnitude of charge present on the ion. e.g:
O(8) = 1s2, 2s2 2 p4
O2- (10) = 1s2, 2s2 2 p6
Effective Nuclear Charge (Slater’s rule)
In a multielectron atom. the electron of the inner-shell decrease the force of attraction exerted by the nucleus on the valence electrons. This is called shielding effect. Due to this, the nuclear charge (Z) actually present on the nucleus, reduces and is called effective nuclear charge (Zeff). It is calculated by using the formula
Zeff = Z – σ
where σ = screening constant
The magnitude of σ is determined by Slater’s rules.
Slater Rules
1. Write the electronic configuration in the following order and groups.
(ls) (2s, 2p) (3s, 3p) (3d), (4.9.4p) (4d) (4f) (5s, 5p) etc
2. Electrons of (/1 + 1) shell (shell higher than considering electrons) do not contribute in shielding i.e., σ = 0
3. All other electrons in (ns, np) group contribute σ = 0.35 each
4. All electrons of (n -1) sand p shell contribute σ = 0.85 each
5 All electrons of (n – 2) sand p shell or lower shell contribute σ = 1.00 each
6. All electrons of nd and nf orbital contribute σ = 0.35 and those of (n – 1)and f or lower orbital contribute σ = 1.00 each
e.g.. Be (4) = 1s2, 2s2
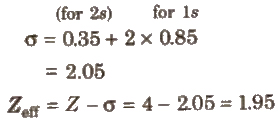
Different Types of Atomic Species
(a) Isotopes Species with same atomic number but different mass number are called isotopes, e.g. , 1H1, 1H2.
(b) Isobars Species with same mass number but different atomic number are called isobars. e.g., 18Ar40, 19K40.
(c) Isotones Species having same number of neutrons are called isotopes, e.g., 1H3 and 2He4 are isotones.
(d) Isodiaphers Species with same isotopic number are called Isodiaphers, e.g., 19K39, 9F19
Isotopic number = mass number – 2 * atomic number .
(e) Isoelectronic Species with same number of electrons are called isoelectronic species, e.g., Na+, Mg2+.
(f) Isostere Species having same number of atoms and same number of electrons, are called isostere, e.g., N2 and CO.
Class 11 Key Points, Important Questions & Practice Papers
Hope these notes helped you in your schools exam preparation. Candidates can also check out the Key Points, Important Questions & Practice Papers for various Subjects for Class 11 in both Hindi and English language form the link below.
Class 11 NCERT Solutions
Candidates who are studying in Class 11 can also check Class 11 NCERT Solutions from here. This will help the candidates to know the solutions for all subjects covered in Class 11th. Candidates can click on the subject wise link to get the same. Class 11 Chapter-wise, detailed solutions to the questions of the NCERT textbooks are provided with the objective of helping students compare their answers with the sample answers.
Class 11 Mock Test / Practice
Mock test are the practice test or you can say the blue print of the main exam. Before appearing in the main examination, candidates must try mock test as it helps the students learn from their mistakes. With the help of Class 11 Mock Test / Practice, candidates can also get an idea about the pattern and marking scheme of that examination. For the sake of the candidates we are providing Class 11 Mock Test / Practice links below.
Class 11 Exemplar Questions
Exemplar Questions Class 11 is a very important resource for students preparing for the Examination. Here we have provided Exemplar Problems Solutions along with NCERT Exemplar Problems Class 11. Question from very important topics is covered by Exemplar Questions for Class 11.
CBSE Notes for Class 11 Chemistry Maths Notes Physics Notes Biology Notes
To get study material, exam alerts and news, join our Whatsapp Channel.



