Class 11 Physics Vectors – Get here the Notes for Class 11 Physics Vectors. Candidates who are ambitious to qualify the Class 11 with good score can check this article for Notes. This is possible only when you have the best CBSE Class 11 Physics study material and a smart preparation plan. To assist you with that, we are here with notes. Hope these notes will helps you understand the important topics and remember the key points for exam point of view. Below we provided the Notes of Class 11 Physics for topic Vectors.
- Class: 11th
- Subject: Physics
- Topic: Vectors
- Resource: Notes
CBSE Notes Class 11 Physics Vectors
Candidates who are pursuing in Class 11 are advised to revise the notes from this post. With the help of Notes, candidates can plan their Strategy for particular weaker section of the subject and study hard. So, go ahead and check the Important Notes for Class 11 Physics Vectors from this article.
Those physical quantities which require magnitude as well as direction for their complete representation and follows vector laws are called vectors.
Vector can be divided into two types
1. Polar Vectors
These are those vectors which have a starting point or a point of application as a displacement, force etc.
2. Axial Vectors
These are those vectors which represent rotational effect and act along the axis of rotation in accordance with right hand screw rule as angular velocity, torque, angular momentum etc.
Scalars
Those physical quantities which require only magnitude but no direction for their complete representation, are called scalars.
Distance, speed, work, mass, density, etc are the examples of scalars. Scalars can be added, subtracted, multiplied or divided by simple algebraic laws.
Tensors
Tensors are those physical quantities which have different values in different directions at the same point.
Moment of inertia, radius of gyration, modulus of elasticity, pressure, stress, conductivity, resistivity, refractive index, wave velocity and density, etc are the examples of tensors. Magnitude of tensor is not unique.
Different Types of Vectors
(i) Equal Vectors Two vectors of equal magnitude, in same direction are called equal vectors.

(ii) Negative Vectors Two vectors of equal magnitude but in opposite directions are called negative vectors.

(iii) Zero Vector or Null Vector A vector whose magnitude is zero is known as a zero or null vector. Its direction is not defined. It is denoted by 0.
Velocity of a stationary object, acceleration of an object moving with uniform velocity and resultant of two equal and opposite vectors are the examples of null vector.
(iv) Unit Vector A vector having unit magnitude is called a unit vector.
A unit vector in the direction of vector A is given by
 = A / A
A unit vector is unitless and dimensionless vector and represents direction only.

(v) Orthogonal Unit Vectors The unit vectors along the direction of orthogonal axis, i.e., X – axis, Y – axis and Z – axis are called orthogonal unit vectors. They are represented by
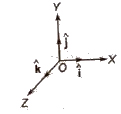
(vi) Co-initial Vectors Vectors having a common initial point, are called co-initial vectors.
(vii) Collinear Vectors Vectors having equal or unequal magnitudes but acting along the same or Ab parallel lines are called collinear vectors.

(viii) Coplanar Vectors Vectors acting in the same plane are called coplanar vectors.
(ix) Localised Vector A vector whose initial point is fixed, is called a localised vector.
(x) Non-localised or Free Vector A vector whose initial point is not fixed is called a non-localised or a free vector.
(xi) Position Vector A vector representing the straight line distance and the direction of any point or object with respect to the origin, is called position vector.
Addition of Vectors
1. Triangle Law of Vectors
If two vectors acting at a point are represented in magnitude and direction by the two sides of a triangle taken in one order, then their resultant is represented by the third side of the triangle taken in the opposite order.
If two vectors A and B acting at a point are inclined at an angle θ, then their resultant
R = √A2 + B2 + 2AB cos θ
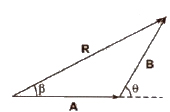
If the resultant vector R subtends an angle β with vector A, then
tan β = B sin θ / A + B cos θ
2. Parallelogram Law of Vectors
If two vectors acting at a point are represented in magnitude and direction by the two adjacent sides of a parallelogram draw from a point, then their resultant is represented in magnitude and direction by the diagonal of the parallelogram draw from the same point.
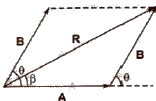
Resultant of vectors A and B is given by
√A2 + B2 + 2AB cos θ
If the resultant vector R subtends an angle β with vector A, then
tan β = B sin θ / A + B cos θ
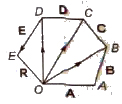
Polygon Law of Vectors
It states that if number of vectors acting on a particle at a time are represented in magnitude and – direction by the various sides of an open polygon taken in same order, their resultant vector E is represented in magnitude and direction by the closing side of polygon taken in opposite order. In fact, polygon law of vectors is the outcome of triangle law of vectors.
R = A + B + C + D + E
OE = OA + AB + BC + CD + DE
Properties of Vector Addition
(i) Vector addition is commutative, i.e., A + B = B + A
(ii) Vector addition is associative, i.e.,
A +(B + C)= B + (C + A)= C + (A + B)
(iii) Vector addition is distributive, i.e., m (A + B) = m A + m B
Rotation of a Vector
(i) If a vector is rotated through an angle 0, which is not an integral multiple of 2 π, the vector changes.
(ii) If the frame of reference is rotated or translated, the given vector does not change. The components of the vector may, however, change.
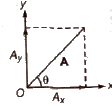
Resolution of a Vector into Rectangular Components
If any vector A subtends an angle θ with x-axis, then its
Horizontal component Ax = A cos θ
Vertical component Ay = A sin θ
Magnitude of vector A = √Ax2 + Ay2
tan θ = Ay / Ax
Direction Cosines of a Vector
If any vector A subtend angles α, β and γ with x – axis, y – axis and z – axis respectively and its components along these axes are Ax, Ay and Az, then
cos α= Ax / A, cos β = Ay / A, cos γ = Az / A
and cos2 α + cos2 β + cos2 γ = 1
Subtraction of Vectors
Subtraction of a vector B from a vector A is defined as the addition of vector -B (negative of vector B) to vector A
Thus, A – B = A + (-B)
Multiplication of a Vector
1. By a Real Number
When a vector A is multiplied by a real number n, then its magnitude becomes n times but direction and unit remains unchanged.
2. By a Scalar
When a vector A is multiplied by a scalar S, then its magnitude becomes S times, and unit is the product of units of A and S but direction remains same as that of vector A.
Scalar or Dot Product of Two Vectors
The scalar product of two vectors is equal to the product of their magnitudes and the cosine of the smaller angle between them. It is denoted by . (dot).
A * B = AB cos θ

The scalar or dot product of two vectors is a scalar.
Properties of Scalar Product
(i) Scalar product is commutative, i.e., A * B= B * A
(ii) Scalar product is distributive, i.e., A * (B + C) = A * B + A * C
(iii) Scalar product of two perpendicular vectors is zero.
A * B = AB cos 90° = O
(iv) Scalar product of two parallel vectors is equal to the product of their magnitudes, i.e., A * B = AB cos 0° = AB
(v) Scalar product of a vector with itself is equal to the square of its magnitude, i.e.,
A * A = AA cos 0° = A2
(vi) Scalar product of orthogonal unit vectors
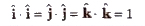

and
(vii) Scalar product in cartesian coordinates
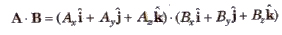
= AxBx + AyBy + AzBz
Vector or Cross Product of Two Vectors
The vector product of two vectors is equal to the product of their magnitudes and the sine of the smaller angle between them. It is denoted by * (cross).
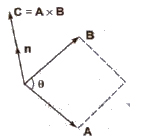
A * B = AB sin θ n
The direction of unit vector n can be obtained from right hand thumb rule.
If fingers of right hand are curled from A to B through smaller angle between them, then thumb will represent the direction of vector (A * B).
The vector or cross product of two vectors is also a vector.
Properties of Vector Product
(i) Vector product is not commutative, i.e.,
A * B ≠ B * A [∴ (A * B) = — (B * A)]
(ii) Vector product is distributive, i.e.,
A * (B + C) = A * B + A * C
(iii) Vector product of two parallel vectors is zero, i.e.,
A * B = AB sin O° = 0
(iv) Vector product of any vector with itself is zero.
A * A = AA sin O° = 0
(v) Vector product of orthogonal unit vectors
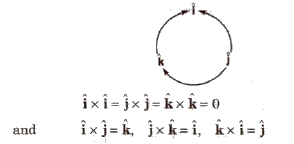
(vi) Vector product in cartesian coordinates
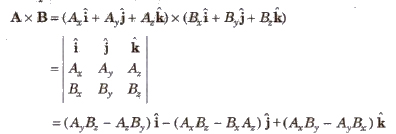
Direction of Vector Cross Product
When C = A * B, the direction of C is at right angles to the plane containing the vectors A and B. The direction is determined by the right hand screw rule and right hand thumb rule.
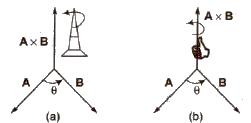
(i) Right Hand Screw Rule Rotate a right handed screw from first vector (A) towards second vector (B). The direction in which the right handed screw moves gives the direction of vector (C).
(ii) Right Hand Thumb Rule Curl the fingers of your right hand from A to B. Then, the direction of the erect thumb will point in the direction of A * B.
Class 11 Key Points, Important Questions & Practice Papers
Hope these notes helped you in your schools exam preparation. Candidates can also check out the Key Points, Important Questions & Practice Papers for various Subjects for Class 11 in both Hindi and English language form the link below.
Class 11 NCERT Solutions
Candidates who are studying in Class 11 can also check Class 11 NCERT Solutions from here. This will help the candidates to know the solutions for all subjects covered in Class 11th. Candidates can click on the subject wise link to get the same. Class 11 Chapter-wise, detailed solutions to the questions of the NCERT textbooks are provided with the objective of helping students compare their answers with the sample answers.
Class 11 Mock Test / Practice
Mock test are the practice test or you can say the blue print of the main exam. Before appearing in the main examination, candidates must try mock test as it helps the students learn from their mistakes. With the help of Class 11 Mock Test / Practice, candidates can also get an idea about the pattern and marking scheme of that examination. For the sake of the candidates we are providing Class 11 Mock Test / Practice links below.
Class 11 Exemplar Questions
Exemplar Questions Class 11 is a very important resource for students preparing for the Examination. Here we have provided Exemplar Problems Solutions along with NCERT Exemplar Problems Class 11. Question from very important topics is covered by Exemplar Questions for Class 11.
CBSE Notes for Class 11 Physics Notes Biology Notes Maths Notes Chemistry Notes
To get study material, exam alerts and news, join our Whatsapp Channel.

