Candidates can download NCERT Exemplar Class 11 Maths Unit 3 from this page. The exemplar has been provided by the National Council of Educational Research & Training (NCERT) and the candidates can check it from below for free of cost. It contains objective, very short answer type, short answer type, and long answer type questions. Along with it, the answer for each question has also been provided. From the NCERT Exemplar Class 11 Maths Unit 3, candidates can understand the level and type of questions that are asked in the exam.
NCERT Exemplar Class 11 Maths Unit 3 Trigonometric Functions
NCERT Exemplar Class 11 Maths Unit 3 is for Trigonometric Functions. The type of questions that will be asked from NCERT Class 11 Maths Unit 3 are displayed in the below provided NCERT Exemplar Class 11 Maths Unit 3. With the help of it, candidates can prepare well for the examination.
Also Check: NCERT Solutions for Class 11 Mathematics
3.1 Overview
3.1.1 The word ‘trigonometry’ is derived from the Greek words ‘trigon’ and ‘metron’ which means measuring the sides of a triangle. An angle is the amount of rotation of a revolving line with respect to a fixed line. If the rotation is in clockwise direction the angle is negative and it is positive if the rotation is in the anti-clockwise direction. Usually we follow two types of conventions for measuring angles, i.e., (i) Sexagesimal system (ii) Circular system.
In sexagesimal system, the unit of measurement is degree. If the rotation from the initial to terminal side is 1/360th of a revolution, the angle is said to have a measure of 1°. The classifications in this system are as follows:
1° = 60′
1′ = 60′′
In circular system of measurement, the unit of measurement is radian. One radian is the angle subtended, at the centre of a circle, by an arc equal in length to the radius of the circle. The length s of an arc PQ of a circle of radius r is given by s = rθ, where θ is the angle subtended by the arc PQ at the centre of the circle measured in terms of radians.
3.1.2 Relation between degree and radian
The circumference of a circle always bears a constant ratio to its diameter. This constant ratio is a number denoted by π which is taken approximately as 22/7 for all practical purpose. The relationship between degree and radian measurements is as follows:
2 right angle = 180° = π radians
1 radian = 180°/π = 57°16′ (approx)
1° = π/180 radian = 0.01746 radians (approx)
3.1.3 Trigonometric functions
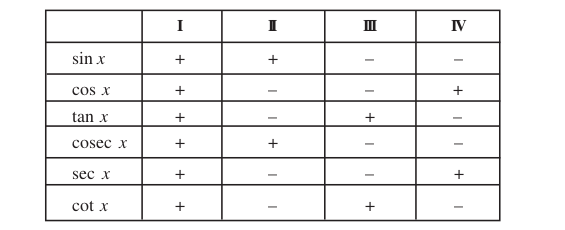
Trigonometric ratios are defined for acute angles as the ratio of the sides of a right angled triangle. The extension of trigonometric ratios to any angle in terms of radian measure (real numbers) are called trigonometric functions. The signs of trigonometric functions in different quadrants have been given in the following table:
3.1.4 Domain and range of trigonometric functions

3.1.5 Sine, cosine and tangent of some angles less than 90°

3.1.6 Allied or Related Angles
The angles (n π/2) ± θ are called allied or related angles and θ ± n × 360° are called coterminal angles. For general reduction, we have the following rules. The value of any trigonometric function for ( nπ/2 ± θ ) is numerically
equal to
(a) the value of the same function if n is an even integer with algebaric sign of the function as per the quadrant in which angles lie.
(b) corresponding cofunction of θ if n is an odd integer with algebraic sign of the function for the quadrant in which it lies. Here sine and cosine; tan and cot; sec and cosec are cofunctions of each other.
3.1.7 Functions of negative angles Let θ be any angle. Then
sin (– θ) = – sin θ, cos (– θ) = cos θ
tan (– θ) = – tan θ, cot (– θ) = – cot θ
sec (– θ) = sec θ, cosec (– θ) = – cosec θ
3.1.8 Some formulae regarding compound angles
An angle made up of the sum or differences of two or more angles is called a compound angle. The basic results in this direction are called trigonometric identies as given below:




Trigonometric functions of an angle of 18°

3.1.9 Trigonometric equations
Equations involving trigonometric functions of a variables are called trigonometric equations. Equations are called identities, if they are satisfied by all values of the unknown angles for which the functions are defined. The solutions of a trigonometric equations for which 0 ≤ θ < 2 π are called principal solutions. The expression involving integer n which gives all solutions of a trigonometric equation is called the
general solution.
General Solution of Trigonometric Equations

Short Answer Type Questions (Solved Examples)








Long Answer Type Questions (Solved Examples)


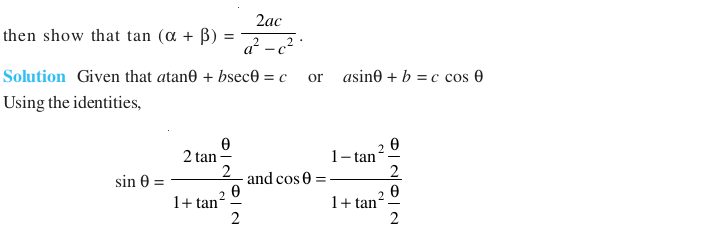

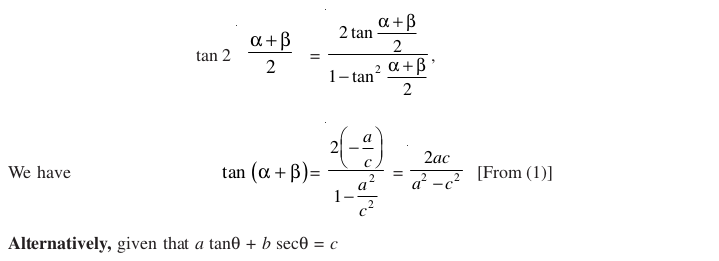



Objective Type Questions (Solved Examples)




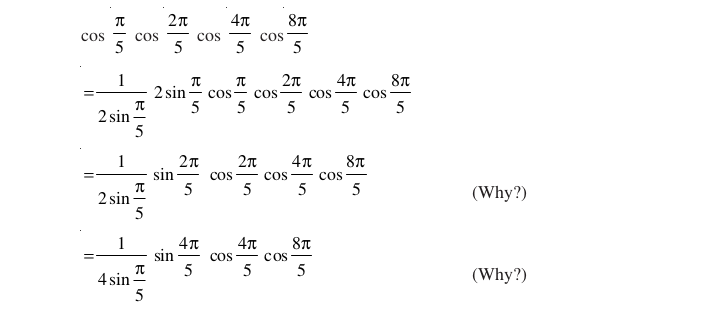

Fill in the blanks type questions (Solved Examples)


Match Type Questions (Solved Examples)


Short Answer Type Questions (Exercise)

Long Answer Type Questions (Exercise)

Objective Type Questions (Exercise)

Fill In Blanks Type Questions

True or False Statements Type Questions

Match Type Questions

Click Here to download NCERT Exemplar Class 11 Maths Unit 3 Trigonometric Functions
Answers



To get study material, exam alerts and news, join our Whatsapp Channel.

