NCERT Exemplar Class 11 Maths Unit 5 Complex Numbers and Quadratic Equations

Candidates can download NCERT Exemplar Class 11 Maths Unit 5 from this page. The exemplar has been provided by the National Council of Educational Research & Training (NCERT) and the candidates can check it from below for free of cost. It contains objective, very short answer type, short answer type, and long answer type questions. Along with it, the answer for each question has also been provided. From the NCERT Exemplar Class 11 Maths Unit 5, candidates can understand the level and type of questions that are asked in the exam. 

NCERT Exemplar Class 11 Maths Unit 5 Complex Numbers and Quadratic Equations – PDF Download

Read Online

NCERT Exemplar Class 11 Maths Unit 5 Complex Numbers And Quadratic Equations Open PDF

NCERT Exemplar Class 11 Maths Unit 5 Complex Numbers and Quadratic Equations

NCERT Exemplar Class 11 Maths Unit 5 is for Complex Numbers and Quadratic Equations. The type of questions that will be asked from NCERT Class 11 Maths Unit 5 are displayed in the below provided NCERT Exemplar Class 11 Maths Unit 5. With the help of it, candidates can prepare well for the examination.

Also Check: NCERT Solutions for Class 11 Mathematics

5.1 Overview
We know that the square of a real number is always non-negative e.g.  4² = 16 and  (– 4)² = 16. Therefore, square root of 16 is ± 4. What about the square root of a negative number? It is clear that a negative number can not have a real square root. So we need to extend the system of real numbers to a system in which we can find out the square roots of negative numbers. Euler (1707 – 1783) was the first mathematician to introduce the symbol i (iota) for positive square root of – 1 i.e., i =

5.1.1 Imaginary numbers
Square root of a negative number is called an imaginary number., for example,

5.1.2 Integral powers of i

5.1.3 Complex numbers

a) A number which can be written in the form a + ib, where a, b are real numbers
and i =  is called a complex number.
(b) If z = a + ib is the complex number, then a and b are called real and imaginary parts, respectively, of the complex number and written as Re (z) = a, Im (z) = b.
(c) Order relations “greater than” and “less than” are not defined for complex numbers.
(d) If the imaginary part of a complex number is zero, then the complex number is known as purely real number and if real part is zero, then it is called purely imaginary number, for example, 2 is a purely real number because its imaginary part is zero and 3i is a purely imaginary number because its real part
is zero.

5.1.4 Algebra of complex numbers

5.1.5 Addition of complex numbers satisfies the following properties

5.1.6 Multiplication of complex numbers

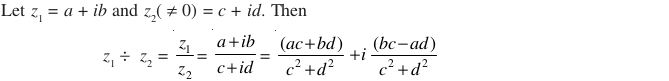
5.1.7

5.1.8 Conjugate of a complex number

5.1.9 Modulus of a complex number

5.1.10 Properties of modulus of a complex number

5.2 Argand Plane
A complex number z = a + ib can be represented by a unique point P (a, b) in the cartesian plane referred to a pair of rectangular axes. The complex number 0 + 0i represent the origin 0 ( 0, 0). A purely real number a, i.e., (a + 0i) is represented by the point (a, 0) on x – axis. Therefore, x-axis is called real axis. A purely imaginary number ib, i.e., (0 + ib) is represented by the point (0, b) on y-axis. Therefore, y-axis is called imaginary axis.
Similarly, the representation of complex numbers as points in the plane is known as Argand diagram. The plane representing complex numbers as points is called complex plane or Argand plane or Gaussian plane.

5.2.1 Polar form of a complex number

5.2.2 Solution of a quadratic equation
The equations ax 2 + bx + c = 0, where a, b and c are numbers (real or complex, a ≠ 0) is called the general quadratic equation in variable x. The values of the variable satisfying the given equation are called roots of the equation.
The quadratic equation ax² + bx + c = 0 with real coefficients has two roots given by    , where D = b² – 4ac, called the discriminant of the equation.

Notes:

• When D = 0, roots of the quadratic equation are real and equal. When D > 0, roots are real and unequal. Further, if a, b, c ∈ Q and D is a perfect square, then the roots of the equation are rational and unequal, and if a, b, c ∈Q and D is not a perfect square, then the roots are irrational and occur in pair.
• When D < 0, roots of the quadratic equation are non real (or complex).
  Let α, β be the roots of the quadratic equation ax² + bx + c = 0, then sum of the roots (α + β) =
  − b/a and the product of the roots ( α . β) =  c/a
• Let S and P be the sum of roots and product of roots, respectively, of a quadratic equation. Then the quadratic equation is given by x² – Sx + P = 0.

Short Answer Type Questions (Solved Examples)

Long Answer Type Questions (Solved Examples)

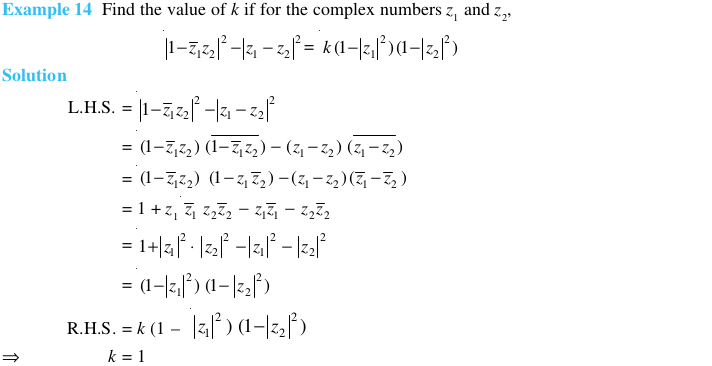
Objective Type Questions (Solved Examples)

Short Answer Type Questions (Exercise)

Long Answer Type Questions (Exercise)

Fill in the Blank Type Questions (Exercise)

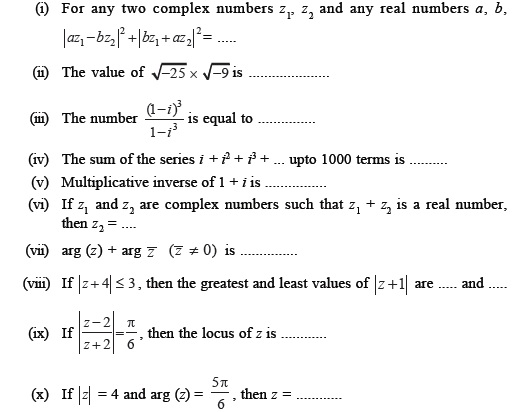
True or False Type Questions (Exercise)

Match Type Questions (Exercise)

Other Questions (Exercise)

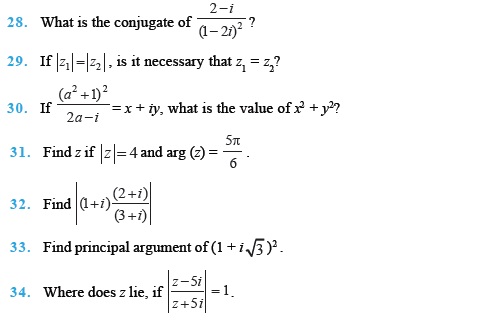
Objective Type Questions (Exercise)

Click Here to download NCERT Exemplar Class 11 Maths Unit 5 Complex Numbers and Quadratic Equations.

Answers

Maths Physics Maths Biology

NCERT Exemplar Class 11 Maths Unit 5 Complex Numbers and Quadratic Equations – FAQs