Candidates can download NCERT Exemplar Class 11 Maths Unit 6 from this page. The exemplar has been provided by the National Council of Educational Research & Training (NCERT) and the candidates can check it from below for free of cost. It contains objective, very short answer type, short answer type, and long answer type questions. Along with it, the answer for each question has also been provided. From the NCERT Exemplar Class 11 Maths Unit 6, candidates can understand the level and type of questions that are asked in the exam.
NCERT Exemplar Class 11 Maths Unit 6 Linear Inequalities
NCERT Exemplar Class 11 Maths Unit 6 is for Linear Inequalities. The type of questions that will be asked from NCERT Class 11 Maths Unit 6 are displayed in the below provided NCERT Exemplar Class 11 Maths Unit 6. With the help of it, candidates can prepare well for the examination.
Also Check: NCERT Solutions for Class 11 Mathematics
6.1 Overview
6.1.1 A statement involving the symbols ‘>’, ‘<’, ‘ ≥’, ‘≤’ is called an inequality. For example 5 > 3, x ≤ 4, x + y ≥ 9.
(i) Inequalities which do not involve variables are called numerical inequalities. For example 3 < 8, 5 ≥ 2.
(ii) Inequalities which involve variables are called literal inequalities. For example, x > 3, y ≤ 5, x – y ≥ 0.
(iii) An inequality may contain more than one variable and it can be linear, quadratic or cubic etc. For eaxmple, 3x – 2 < 0 is a linear inequality in one variable, 2x + 3y ≥ 4 is a linear inequality in two variables and x 2 + 3x + 2 < 0 is a quadratic inequality in one variable.
(iv) Inequalities involving the symbol ‘>’ or ‘<’ are called strict inequalities. For example, 3x – y > 5, x < 3.
(v) Inequalities involving the symbol ‘≥’ or ‘≤’ are called slack inequalities. For
example, 3x – y ≥ 5, x ≤ 5.
6.1.2 Solution of an inequality
(i) The value(s) of the variable(s) which makes the inequality a true statement is called its solutions. The set of all solutions of an inequality is called the solution set of the inequality. For example, x – 1 ≥ 0, has infinite number of solutions as all real values greater than or equal to one make it a true statement. The inequality x2 + 1 < 0 has no solution in R as no real value of x makes it a true statement.
To solve an inequality we can
(i) Add (or subtract) the same quantity to (from) both sides without changing the sign of inequality.
(ii) Multiply (or divide) both sides by the same positive quantity without changing the sign of inequality. However, if both sides of inequality are multiplied (or divided) by the same negative quantity the sign of inequality is reversed, i.e., ‘>’ changes into ‘<’ and vice versa.
6.1.3 Representation of solution of linear inequality in one variable on a number line
To represent the solution of a linear inequality in one variable on a number line, we use the following conventions:
(i) If the inequality involves ‘≥’ or ‘≤’, we draw filled circle (•) on the number line to indicate that the number corresponding to the filled circle is included in the solution set.
(ii) If the inequality involves ‘>’ or ‘<’, we draw an open circle (O) on the number line to indicate that the number corresponding to the open circle is excluded from the solution set.
6.1.4 Graphical representation of the solution of a linear inequality
(a) To represent the solution of a linear inequality in one or two variables graphically in a plane, we proceed as follows:
(i) If the inequality involves ‘≥’ or ‘≤’, we draw the graph of the line as a thick
line to indicate that the points on this line are included in the solution set.
(ii) If the inequality involves ‘>’ or ‘<’, we draw the graph of the line as dotted line to indicate that the points on the line are excluded from the solution set.
(b) Solution of a linear inequality in one variable can be represented on number line as well as in the plane but the solution of a linear inequality in two variables of the type ax + by > c, ax + by ≥ c, ax + by < c or ax + by ≤ c (a ≠ 0, b ≠ 0) can be represented in the plane only.
(c) Two or more inequalities taken together comprise a system of inequalities and the solutions of the system of inequalities are the solutions common to all the inequalities comprising the system.
6.1.5 Two important results
(a) If a, b ∈ R and b ≠ 0, then
(i) ab > 0 or a/b > 0 ⇒ a and b are of the same sign.
(ii) ab < 0 or a/b< 0 ⇒ a and b are of opposite sign.
(b) If a is any positive real number, i.e., a > 0, then
(i) | x | < a ⇔ – a < x < a
|x | ≤ a ⇔ – a ≤ x ≤ a
(ii) | x | > a ⇔ x < – a or x > a
| x | ≥ a ⇔ x ≤ – a or x ≥ a
Short Type Questions (Solved Examples)





Long Type Questions (Solved Examples)




Objective Type Questions (Solved Examples)




Fill in the Blanks Type Questions (Solved Examples)


Short Type Questions (Exercise)

Long Type Questions
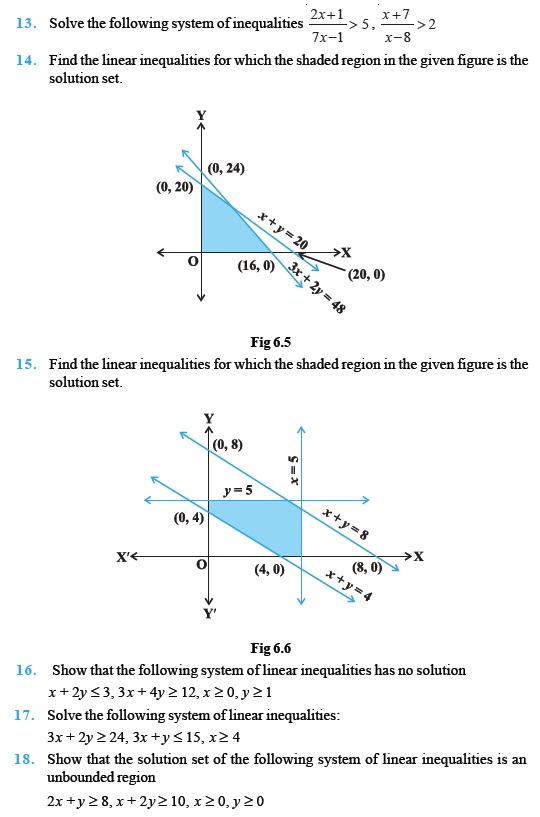
Objective Type Questions

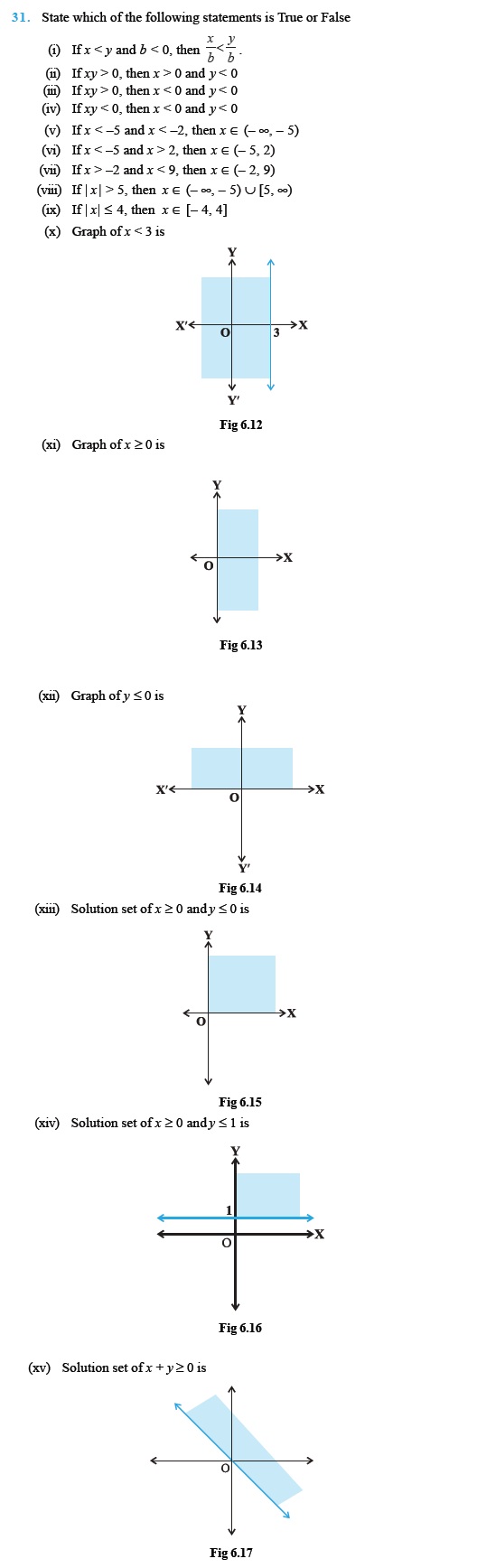
True or False Type Questions
Fill in the Blanks Type Questions

Click Here to download NCERT Exemplar Class 11 Maths Unit 6 Linear Inequalities.
Answers


To get study material, exam alerts and news, join our Whatsapp Channel.
