Candidates can download NCERT Exemplar Class 7 Maths Unit 7 from this page. The exemplar has been provided by the National Council of Educational Research & Training (NCERT) and the candidates can check it from below for free of cost. It contains objective, very short answer type, short answer type, and long answer type questions. Along with it, the answer for each question has also been provided. From the NCERT Exemplar Class 7 Maths Unit 7, candidates can understand the level and type of questions that are asked in the exam.
NCERT Exemplar Class 7 Maths Unit 7 Comparing Quantities
NCERT Class 7 Maths Unit 7 is for Comparing Quantities. The type of questions that will be asked from NCERT Class 7 Maths Unit 7 are displayed in the below provided NCERT Exemplar Class 7 Maths Unit 7. With the help of it, candidates can prepare well for the examination.
Main Concepts and Results
To compare two quantities, their units must be the same.
Two ratios can be compared by converting them into like fractions. If the two fractions are equal, we say that the two given ratios are equivalent.
If two ratios are equivalent (or equal), then the involved four quantities are said to be in proportion.
One of the ways of comparing quantities is percentage. Per cent is derived from Latin word ‘per centum’ meaning ‘per hundred’.
Percent is represented by the symbol % and means hundredth too.
Fractions can be converted into percentages and vice-versa.
Decimals can also be converted into percentages and vice-versa.
The buying price of any item is known as its cost price. It is written in short as CP.
The price at which an item is sold, is known as its selling price or in short SP.
If CP < SP, then a profit is made and Profit = SP – CP.
If CP = SP, there is no profit or loss.
If CP > SP, then a loss is made and Loss = CP – SP.
Profit per cent =
Loss per cent =
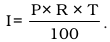
Principal’ P, means the borrowed money.
The extra money paid by borrower for using borrowed money for given time is called ‘Interest’ I.
The period for which the money is borrowed is called ‘Time Period’ T.
To determine Interest to be paid, we have ‘Rate of Interest’.
Rate of Interest is generally given in per cent per year.
On a principal of ₹ P at R % rate of interest per year, the interest (simple) I paid for T years is given by
The total money paid alongwith interest or principal P is called amount (A). Thus A = P + I.
Solved Examples
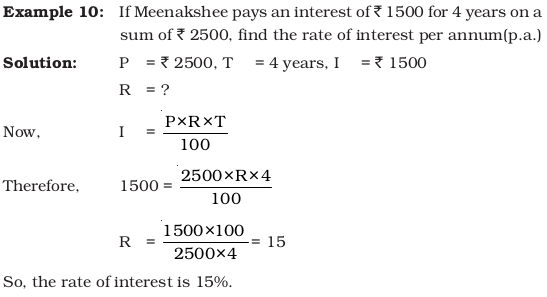
Multiple Choice Questions
Fill in the Blanks Type Questions
True False Type Questions
Other Important Type Questions
Application
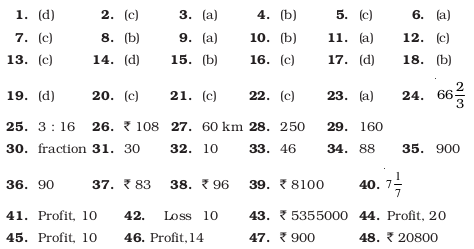
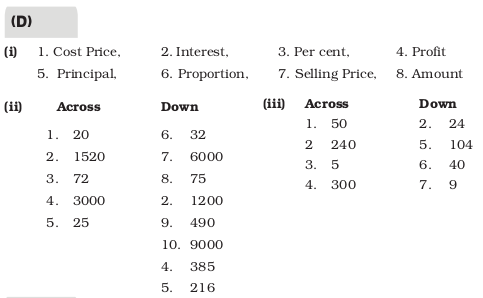
Answers
To get fastest exam alerts and government job alerts in India, join our Telegram channel.
Discussion about this post