NCERT Exemplar Class 12 Mathematics Chapter 12 Linear Programming – the extra practice questions NCERT publishes for the chapter (MCQs, very short, short and long answer questions) with their answers.
NCERT Exemplar Class 12 Mathematics Chapter 12 Linear Programming PDF
| Chapter | Download | |
|---|---|---|
| Exemplar PDF | Linear Programming | View PDF |
Read Online
NCERT Exemplar Class 12 Mathematics Chapter 12 Linear Programming – Questions and Answers
Short Answer Type Questions (Solved Examples)
Long Answer Type Questions (Solved Examples)
Objective Type Questions (Solved Examples)
Short Answer Type Questions (Exercise)
Long Answer Type Questions (Exercise)
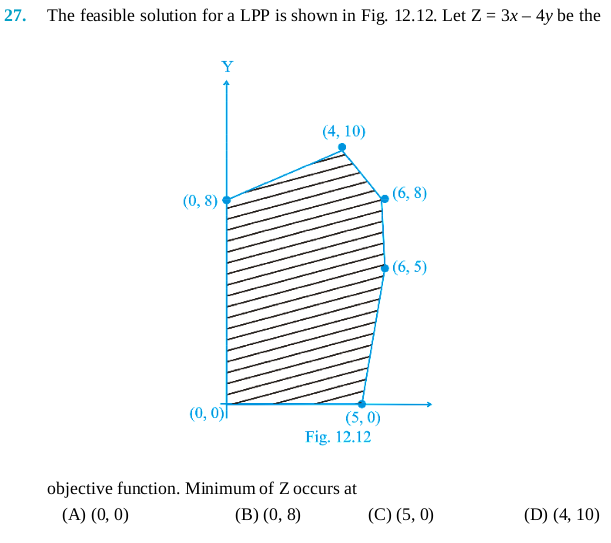
Multiple Choice Questions
Fill In Blanks Type Questions
True or False Statements Type Questions
| « Previous | Next » |
Answers
Maths Physics Chemistry Biology
NCERT Exemplar Class 12 Mathematics Chapter 12 Linear Programming – Overview
| Class | Class 12 |
| Subject | Mathematics |
| Chapter | 12 – Linear Programming |
| Session | 2027 |
| Format | PDF – read online or download |
Chapter 12 of 13 – Mathematics
- Previous: Chapter 11 Three Dimensional Geometry
- Next: Chapter 13 Probability
- All chapters: NCERT Exemplar Class 12 Mathematics
NCERT Exemplar Class 12 Mathematics Chapter 12 Linear Programming – Overview
| Class | Class 12 |
| Subject | Mathematics |
| Chapter | 12 – Linear Programming |
| Session | 2027 |
| Format | PDF – read online or download |
NCERT Exemplar Class 12 Mathematics Chapter 12 – FAQs
Where can I download NCERT Exemplar Class 12 Mathematics Chapter 12 Linear Programming PDF?
From the download table on this page – it is free.
Is this for the 2027 session?
Yes, it follows the latest NCERT Class 12 Mathematics book for 2027.
How should I use these exemplar problems?
Read the chapter in the NCERT book first, attempt the questions yourself, then check your answers here.
Chapter 12 of 13 – Mathematics
- Previous: Chapter 11 Three Dimensional Geometry
- Next: Chapter 13 Probability
- All chapters: NCERT Exemplar Class 12 Mathematics
NCERT Exemplar Class 12 Mathematics Chapter 12 Linear Programming – Overview
| Class | Class 12 |
| Subject | Mathematics |
| Chapter | 12 – Linear Programming |
| Session | 2027 |
| Format | PDF – read online or download |
NCERT Exemplar Class 12 Mathematics Chapter 12 – FAQs
Where can I download NCERT Exemplar Class 12 Mathematics Chapter 12 Linear Programming PDF?
From the download table on this page – it is free.
Is this for the 2027 session?
Yes, it follows the latest NCERT Class 12 Mathematics book for 2027.
How should I use these exemplar problems?
Read the chapter in the NCERT book first, attempt the questions yourself, then check your answers here.
Chapter 12 of 13 – Mathematics
- Previous: Chapter 11 Three Dimensional Geometry
- Next: Chapter 13 Probability
- All chapters: NCERT Exemplar Class 12 Mathematics
NCERT Exemplar Class 12 Mathematics Chapter 12 Linear Programming – Overview
| Class | Class 12 |
| Subject | Mathematics |
| Chapter | 12 – Linear Programming |
| Session | 2027 |
| Format | PDF – read online or download |
NCERT Exemplar Class 12 Mathematics Chapter 12 – FAQs
Where can I download NCERT Exemplar Class 12 Mathematics Chapter 12 Linear Programming PDF?
From the download table on this page – it is free.
Is this for the 2027 session?
Yes, it follows the latest NCERT Class 12 Mathematics book for 2027.
How should I use these exemplar problems?
Read the chapter in the NCERT book first, attempt the questions yourself, then check your answers here.
NCERT Exemplar Class 12 Mathematics Chapter 12 – FAQs
Where can I download NCERT Exemplar Class 12 Mathematics Chapter 12 Linear Programming PDF?
From the download table on this page – it is free.
Is this for the 2027 session?
Yes, it follows the latest NCERT Class 12 Mathematics book for 2027.
How should I use these exemplar problems?
Read the chapter in the NCERT book first, attempt the questions yourself, then check your answers here.