Candidates can download NCERT Exemplar Class 12 Maths Unit 3 from this page. The exemplar has been provided by the National Council of Educational Research & Training (NCERT) and the candidates can check it from below for free of cost. It contains objective, very short answer type, short answer type, and long answer type questions. Along with it, the answer for each question has also been provided. From the NCERT Exemplar Class 12 Maths Unit 3, candidates can understand the level and type of questions that are asked in the exam.
NCERT Exemplar Class 12 Maths Unit 3 Matrices
NCERT Class 12 Maths Unit 3 is for Matrices. The type of questions that will be asked from NCERT Class 12 Maths Unit 3 are displayed in the below provided NCERT Exemplar Class 12 Maths Unit 3. With the help of it, candidates can prepare well for the examination.
Also Check: NCERT Solutions for Class 12 Maths
3.1 Overview
3.1.1 A matrix is an ordered rectangular array of numbers (or functions). For example,
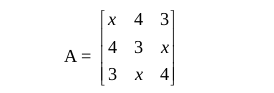
The numbers (or functions) are called the elements or the entries of the matrix. The horizontal lines of elements are said to constitute rows of the matrix and the vertical lines of elements are said to constitute columns of the matrix.
3.1.2 Order of a Matrix
A matrix having m rows and n columns is called a matrix of order m × n or simply m × n matrix (read as an m by n matrix).In the above example, we have A as a matrix of order 3 × 3 i.e., 3 × 3 matrix.
In general, an m × n matrix has the following rectangular array :

The element, aij is an element lying in the ith row and jth column and is known as the (i, j)th element of A. The number of elements in an m × n matrix will be equal to mn.
3.1.3 Types of Matrices
(i) A matrix is said to be a row matrix if it has only one row.
(ii) A matrix is said to be a column matrix if it has only one column.

3.1.4 Additon of Matrices
Two matrices can be added if they are of the same order.
3.1.5 Multiplication of Matrix by a Scalar

3.1.6 Negative of a Matrix
The negative of a matrix A is denoted by –A. We define –A = (–1)A.
3.1.7 Multiplication of Matrices
The multiplication of two matrices A and B is defined if the number of columns of A is equal to the number of rows of B.

Notes:
1. If AB is defined, then BA need not be defined.
2. If A, B are, respectively m × n, k × l matrices, then both AB and BA are defined if and only if n = k and l = m.
3. If AB and BA are both defined, it is not necessary that AB = BA.
4. If the product of two matrices is a zero matrix, it is not necessary that one of the matrices is a zero matrix.
5. For three matrices A, B and C of the same order, if A = B, then AC = BC, but converse is not true.
6. A. A = A2 , A. A. A = A3, so on.
3.1.8 Transpose of a Matrix

3.1.9 Symmetric Matrix and Skew Symmetric Matrix


Note : Diagonal elements of a skew symmetric matrix are zero.

3.1.10 Invertible Matrices

3.1.11 Inverse of a Matrix using Elementary Row or Column Operations

Short Answer Type Questions (Solved Examples)



Long Answer Type Questions (Solved Examples)







Multiple Choice Questions (Solved Examples)



Fill in the Blanks Type Questions (Solved Examples)

True or False Statements Type Questions (Solved Examples)

Short Answer Type Questions (Exercise)

Long Answer Type Questions (Exercise)

Multiple Choice Questions (Exercise)

Fill In Blanks Type Questions (Exercise)

True or False Statements Type Questions (Exercise)

Click Here to download NCERT Exemplar Class 12 Maths Unit 3 Matrices.
Answers



Maths Physics Chemistry Biology
To get study material, exam alerts and news, join our Whatsapp Channel.
