10.1.1 UNIVERSAL LAW OF GRAVITATION
Every object in the universe attracts every other object with a force which is proportional to the product of their masses and inversely proportional to the square of the distance between them. The force is along the line joining the centers of two objects.
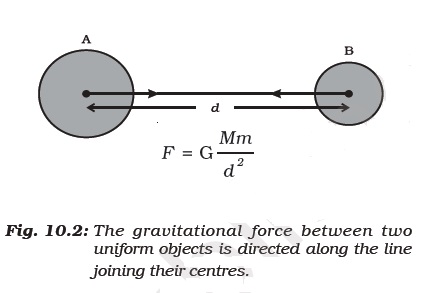
Let two objects A and B of masses M and m lie at a distance d from each other as shown in Fig. 10.2. Let the force of attraction between two objects be F. According to the universal law of gravitation, the force between two objects is directly proportional to the product of their masses. That is,
F ∝ M × m (10.1)
And the force between two objects is inversely proportional to the square of the distance between them, that is,
F ∝ 1/d2 (10.2)
combining Eqs. (10.1) and (10.2), we get
F ∝ M m/d2 (10.3)
or F = G M × m / d2 (10.4)
where G is the constant of proportionality and is called the universal gravitation constant. By multiplying crosswise, Eq. (10.4) gives
F × d2 = G M × m
or G= F d2 / M ×m (10.5)
The SI unit of G can be obtained by substituting the units of force, distance and mass in Eq. (10.5) as N m2 kg-2.
The value of G was found out by Henry Cavendish (1731 – 1810) by using a sensitive balance. The accepted value of G is 6.673 × 10-11 N m2 kg-2.
We know that there exists a force of attraction between any two objects. Compute the value of this force between you and your friend sitting closeby. Conclude how you do not experience this force!
10.1.2 IMPORTANCE OF THE UNIVERSAL LAW OF GRAVITATION
The universal law of gravitation successfully explained several phenomena which were believed to be unconnected:
i. the force that binds us to the earth;
ii. the motion of the moon around the earth
iii. the motion of planets around the Sun and
iv. the tides due to the moon and the Sun.
10.2 Free Fall
We have learnt that the earth attracts objects towards it. This is due to the gravitational force. Whenever objects fall towards the earth under this force alone, we say that the objects are in free fall. Is there any change in the velocity of falling objects? While falling, there is no change in the direction of motion of the objects. But due to the earth’s attraction, there will be a change in the magnitude of the velocity. Any change in velocity involves acceleration. Whenever an object falls towards the earth, an acceleration is involved. This acceleration is due to the earth’s gravitational force. Therefore, this acceleration is called the acceleration due to the gravitational force of the earth (or acceleration due to gravity). It is denoted by g. The unit of g is the same as that of acceleration, that is, m s-2.
We know from the second law of motion that force is the product of mass and acceleration. Let the mass of the stone in activity 10.2 be m. We already know that there is acceleration involved in falling objects due to the gravitational force and is denoted by g. Therefore the magnitude of the gravitational force F will be equal to the product of mass and acceleration due to the gravitational force, that is,
F = m g (10.6)
From Eqs. (10.4) and (10.6) we have
mg = G M× m / d2
or g = G M / d2 (10.7)
where M is the mass of the earth, and d is the distance between the object and the earth.
Let an object be on or near the surface of the earth. The distance d in Eq. (10.7) will be equal to R, the radius of the earth. Thus, for objects on or near the surface of the earth,
mg = G M× m / R2 (10.8)
or g =G M/R2 (10.9)
The earth is not a perfect sphere. As the radius of the earth increases from the poles to the equator, the value of g becomes greater at the poles than at the equator. For most calculations, we can take g to be more or less constant on or near the earth. But for objects far from the earth, the acceleration due to gravitational force of earth is given by Eq.(10.7).
10.2.1 TO CALCULATE THE VALUE OF g
To calculate the value of g, we should put the values of G, M and R in Eq. (10.9), namely, universal gravitational constant, G = 6.7 × 10-11 N m2 kg-2, mass of the earth, M = 6 × 1024 kg, and radius of the earth,
R = 6.4 × 106 m.
g = G M/R2
= G 6.7 × 10-11 M2Kg-2 × 6 ×1024 / {(6.4 ×106)m}2
= 9.8 ms-2.
Thus, the value of acceleration due to gravity of the earth, g = 9.8 m s-2.
10.2.2 MOTION OF OBJECTS UNDER THE INFLUENCE OF GRAVITATIONAL FORCE OF THE EARTH
We know that an object experiences acceleration during free fall. From Eq. (10.9), this acceleration experienced by an object is independent of its mass. This means that all objects hollow or solid, big or small, should fall at the same rate. According to a story, Galileo dropped different objects from the top of the Leaning Tower of Pisa in Italy to prove the same.
As g is constant near the earth, all the equations for the uniformly accelerated motion of objects become valid with acceleration a replaced by g (see section 8.5).
The equations are:
v = u + at (10.10)
s = ut + ½ a t2 (10.11)
v2 = u2 + 2as (10.12)
where u and v are the initial and final velocities and s is the distance covered in time, t. In applying these equations, we will take acceleration, a to be positive when it is in the direction of the velocity, that is, in the direction of motion. The acceleration, a will be taken as negative when it opposes the motion.
Click Here for All Open Educational Resources
To get fastest exam alerts and government job alerts in India, join our Telegram channel.
