Candidates can download NCERT Exemplar Class 12 Maths Unit 6 from this page. The exemplar has been provided by the National Council of Educational Research & Training (NCERT) and the candidates can check it from below for free of cost. It contains objective, very short answer type, short answer type, and long answer type questions. Along with it, the answer for each question has also been provided. From the NCERT Exemplar Class 12 Maths Unit 6, candidates can understand the level and type of questions that are asked in the exam.
NCERT Exemplar Class 12 Maths Unit 6 Application of Derivatives
NCERT Class 12 Maths Unit 6 is for Application of Derivatives. The type of questions that will be asked from NCERT Class 12 Maths Unit 6 are displayed in the below provided NCERT Exemplar Class 12 Maths Unit 6. With the help of it, candidates can prepare well for the examination.
Also Check: NCERT Solutions for Class 12 Maths
6.1 Overview
6.1.1 Rate of change of quantities

6.1.2 Tangents and normals
A line touching a curve y = f (x) at a point (x1 , y1) is called the tangent to the curve at that point and its equation is given
 .
.
The normal to the curve is the line perpendicular to the tangent at the point of contact, and its equation is given as:

The angle of intersection between two curves is the angle between the tangents to the curves at the point of intersection.
6.1.3 Approximation

6.1.4 Increasing/decreasing functions
A continuous function in an interval (a, b) is :
(i) strictly increasing if for all x 1 , x 2 ∈ (a, b), x 1 < x 2 ⇒ f (x 1 ) < f (x 2 ) or for all x ∈ (a, b), f ′ (x) > 0
(ii) strictly decreasing if for all x 1 , x 2 ∈ (a, b), x 1 < x 2 ⇒ f (x 1 ) > f (x 2 ) or for all x ∈ (a, b), f ′(x) < 0
6.1.5 Theorem : Let f be a continuous function on [a, b] and differentiable in (a, b) then
(i) f is increasing in [a, b] if f ′ (x) > 0 for each x ∈ (a, b)
(ii) f is decreasing in [a, b] if f ′ (x) < 0 for each x ∈ (a, b)
(iii) f is a constant function in [a, b] if f ′ (x) = 0 for each x ∈ (a, b).
6.1.6 Maxima and minima
Local Maximum/Local Minimum for a real valued function f
A point c in the interior of the domain of f, is called
(i) local maxima, if there exists an h > 0 , such that f (c) > f (x), for all x in (c – h, c + h).
The value f (c) is called the local maximum value of f
(ii) local minima if there exists an h > 0 such that f (c) < f (x), for all x in (c – h, c + h).
The value f (c) is called the local minimum value of
A function f defined over [a, b] is said to have maximum (or absolute maximum) at x = c, c ∈ [a, b], if f (x) ≤ f (c) for all x ∈ [a, b].
Similarly, a function f (x) defined over [a, b] is said to have a minimum [or absolute minimum] at x = d, if f (x) ≥ f (d) for all x ∈ [a, b].
6.1.7 Critical point of f : A point c in the domain of a function f at which either f ′ (c) = 0 or f is not differentiable is called a critical point of f.
Working rule for finding points of local maxima or local minima:
(a) First derivative test:
(i) If f ′ (x) changes sign from positive to negative as x increases through c, then c is a point of local maxima, and f (c) is local maximum value.
(ii) If f ′ (x) changes sign from negative to positive as x increases through c, then c is a point of local minima, and f (c) is local minimum value.
(iii) If f ′ (x) does not change sign as x increases through c, then c is neither a point of local minima nor a point of local maxima. Such a point is called a point of inflection.
(b) Second Derivative test: Let f be a function defined on an interval I and c ∈ I. Let f be twice differentiable at c. Then
(i) x = c is a point of local maxima if f ′(c) = 0 and f ″(c) < 0. In this case f (c) is then the local maximum value.
(ii) x = c is a point of local minima if f ′ (c) = 0 and f ″(c) > 0. In this case f (c) is the local minimum value.
(iii) The test fails if f ′(c) = 0 and f ″ (c) = 0. In this case, we go back to first derivative test.
6.1.8 Working rule for finding absolute maxima and or absolute minima :
Step 1 : Find all the critical points of f in the given interval.
Step 2 : At all these points and at the end points of the interval, calculate the values of f.
Step 3 : Identify the maximum and minimum values of f out of the values calculated in step 2. The maximum value will be the absolute maximum value of f and the minimum value will be the absolute minimum value of f.
Short Answer Type Questions (Solved Examples)










Long Answer Type Questions (Solved Examples)










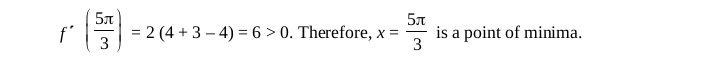







Objective Type Questions (Solved Examples)
Choose the correct answer from the given four options in each of the following Examples
19 to 23.




Fill in the Blanks Type Questions (Solved Examples)

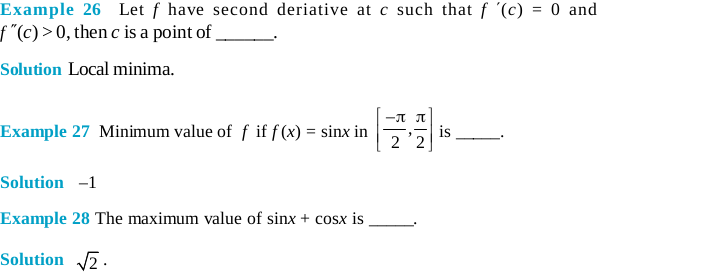

Short Answer Type Questions




Long Answer Type Questions


Multiple Choice Questions







Fill In Blanks Type Questions

| « Previous | Next » |
Answers



Maths Physics Chemistry Biology
To get study material, exam alerts and news, join our Whatsapp Channel.

