ICSE Maths Syllabus 2024 has been released by CISCE. If you are studying Maths in class 9 or 10 in CISCE board, then you can check this ICSE Syllabus to know list of topics to refer from ICSE Maths book. This curriculum includes ICSE Class 10 Maths Syllabus PDF, as well as ICSE Class 9 Maths Syllabus PDF. Therefore you should study all chapters given in this Maths syllabus to be ready for ICSE Maths exams.
ICSE Maths Syllabus 2024
The CISCE syllabus for ICSE (Class 10, and 9) is as follows.
ICSE Maths Syllabus 2024 PDF Download Link – Click Here to Download Syllabus
Note that the ICSE Syllabus 2023-24 or the ICSE 9 syllabus 2023-24 and ICSE 10 syllabus 2023-24 are the topics taught during March/April 2023 to March/April 2024 for CISCE exams 2024. Likewise the ICSE Syllabus 2024-25 is the list of topics you study from March/April 2024 to March/April 2025 for CISCE board exams 2025. Also that in for some subjects, in certain years, CISCE does not publish class 9/10 curriculum for Maths separately. In those years it is assumed that the Maths study topics remain same.
ICSE Maths Syllabus 2024 PDF
The complete course is as follows.
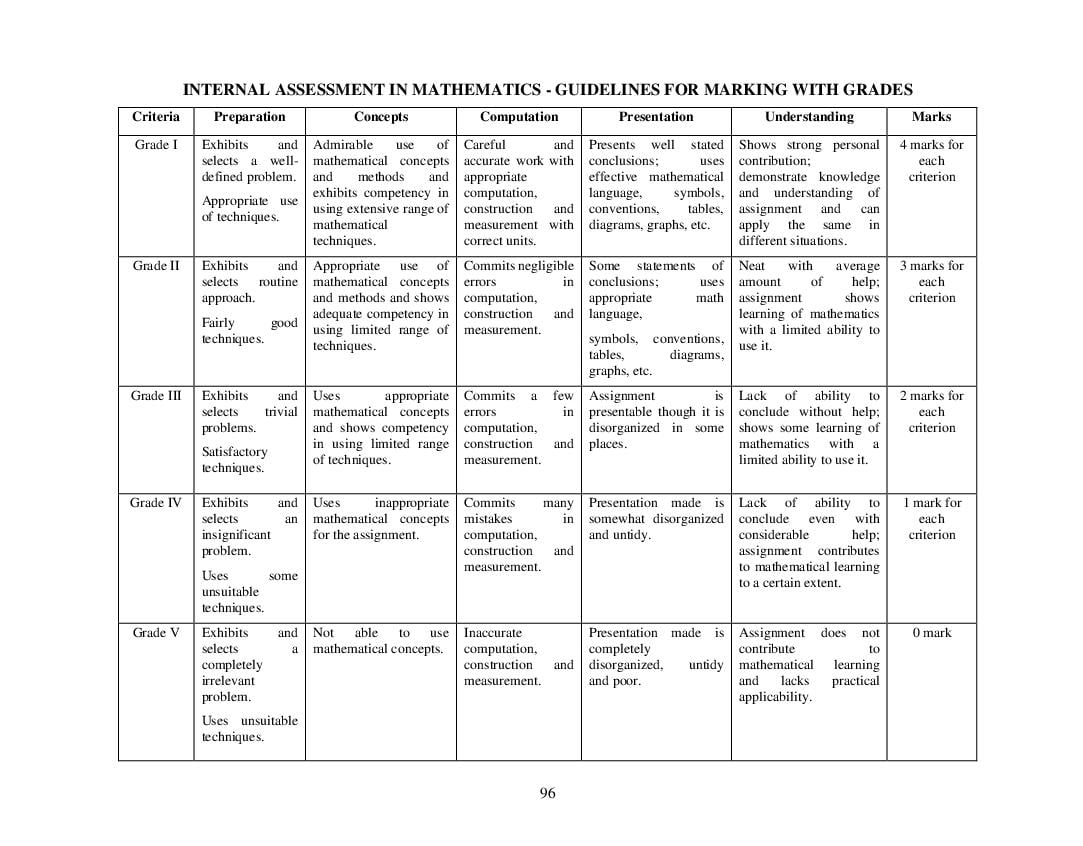
ICSE Class 10 Syllabus 2024 Mathematics View Download









ICSE Syllabus
There are more subjects to study in 9th, and 10th standards in addition to Maths. So here are the subject-wise curriculum for ICSE.
- Art
- Beauty and Wellness – Hair Styling
- Beauty and Wellness – Skin and Beauty
- Biology
- Chemistry
- Classical Language
- Commercial Applications
- Commercial Studies
- Computer Applications
- Cookery
- Economic Applications
- Economics
- English
- Environmental Applications
- Environmental Science
- Fashion Designing
- French
- Geography
- German
- History Civics
- Home Science
- Hospitality Management
- Indian Languages
- Mass Media and Communication
- Maths
- Modern Foreign Languages Group I
- Modern Foreign Languages Group II
- Modern Foreign Languages Group III
- Performing Arts
- Physical Education
- Physics
- Sanskrit
- Spanish
- Supw and Community Service
- Technical Drawing Applications
- Yoga
CISCE Board Syllabus
Likewise you can check the curriculum for other classes, as follows.
ICSE Class 10 Maths
- If you are in 10th standard in CISCE school, then you need to refer ICSE Class 10 Maths Book to study all topics from syllabus.
- Moreover you can use Selina Solutions for 10 Maths to overcome difficulties of exercises.
- Then before exam, solve ICSE Class 10 Maths Specimen Paper 2024 and ICSE Class 10 Maths previous year question papers to get an idea of what to expect in exam.
- Also refer Class 10 Maths notes for CISCE board to revise the topics.
ICSE Class 9 Maths
- Similarly those in 9th standard should study all syllabus topics from ICSE Class 9 Maths Textbook.
- The Selina Solutions for 9 Maths can be used to solve chapter questions and answers.
- In addition the study material like ICSE Class 9 Maths Specimen Paper 2024, and ICSE Class 9 Maths previous year question papers are critical just before final exams.
- And ultimately Class 9 Maths notes come in handy for quick revision.
ICSE Maths Syllabus – An Overview
The following are important details about this curriculum.
| Aspects | Details |
|---|---|
| Education Board | CISCE Board |
| Classes | ICSE (Class 10, 9) |
| Subject | Maths |
| ICSE Full Form | Indian Certificate of Secondary Education |
| Study Resource Here | CISCE Syllabus for Class 10, 9 Maths |
| All Curriculum for This Class | CISCE Syllabus for Class 10, 9 |
| Complete Curriculum for This Board | CISCE Syllabus |
| Exam Dates | ICSE Time Table |
| Results | ICSE Result |
| Previous Year Question Papers | ICSE Previous Year Question Papers |
| Class 10 Sample Papers | ICSE Class 10 Specimen Papers |
| Class 9 Sample Papers | ICSE Class 9 Specimen Papers |
| Official Website for ICSE Maths Syllabus | cisce.org |
If you have any queries on ICSE Maths Syllabus 2024, then please ask in comments below.
To get study material, exam alerts and news, join our Whatsapp Channel.


